题目内容
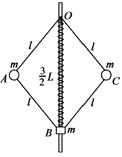
【题目】一转动装置如图所示，四根轻杆OA、OC、AB和CB与两小球以及一小环通过铰链连接，轻杆长均为l，球和环的质量均为m，O端固定在竖直的轻质转轴上，套在转轴上的轻质弹簧连接在O与小环之间，原长为L，装置静止时，弹簧长为
，转动该装置并缓慢增大转速，小环缓慢上升．弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g，求
（1）弹簧的劲度系数k；
（2）AB杆中弹力为零时，装置转动的角速度
；
（3）弹簧长度从缓慢缩短为
的过程中，外界对转动装置所做的功W．
【答案】（1）
；（2）
；（3）
【解析】
（1）装置静止时，设OA、AB杆中的弹力分别为F1、T1，OA杆与转轴的夹角为θ1
小环受到弹簧的弹力
小环受力平衡
F弹1=mg+2T1cosθ1
小球受力平衡
F1cosθ1+T1cosθ1=mg
F1sinθ1=T1sinθ1
解得
（2）设OA、AB杆中的弹力分别为F2、T2，OA杆与转轴的夹角为θ2
小环受到弹簧的弹力
F弹2=k（x-L）
小环受力平衡
F弹2=mg
解得
对小球
F2cosθ2=mg
且
解得
（3）弹簧长度为
时，设OA、AB杆中的弹力分别为F3、T3，OA杆与弹簧的夹角为θ3
小环受到弹簧的弹力
小环受力平衡
2T3cosθ3=mg+F弹3
且
对小球
F3cosθ3=T3cosθ3+mg
解得
整个过程弹簧弹性势能变化为零，则弹力做的功为零，由动能定理：
解得
练习册系列答案
相关题目
