题目内容
 (2006?宿迁三模)如图所示,位于竖直平面内有
(2006?宿迁三模)如图所示,位于竖直平面内有| 1 | 4 |
(1)钢球运动到B点的瞬间受到的支持力多大?
(2)钢球落地点C距B点的水平距离s为多少?
分析:只有重力做功,根据机械能守恒定律列式求解;
做平抛运动,根据平抛运动的位移公式求解;
做平抛运动,根据平抛运动的位移公式求解;
解答:解:(1)由光滑圆弧轨道滑下,机械能守恒,设小球滑到圆弧轨道下端时速度为v1,则:
mgR=
mvB2
解得vB=
即物块A滑到圆弧轨道下端时的速度大小为
.
根据牛顿第二定律得:
F-mg=m
F=3mg
(2)根据平抛运动的规律得:
H-R=
gt2
S=vBt
S=2
答:(1)钢球运动到B点的瞬间受到的支持力为3mg;
(2)钢球落地点C距B点的水平距离为2
.
mgR=
| 1 |
| 2 |
解得vB=
| 2gR |
即物块A滑到圆弧轨道下端时的速度大小为
| 2gR |
根据牛顿第二定律得:
F-mg=m
| ||
| R |
F=3mg
(2)根据平抛运动的规律得:
H-R=
| 1 |
| 2 |
S=vBt
S=2
| R(H-R) |
答:(1)钢球运动到B点的瞬间受到的支持力为3mg;
(2)钢球落地点C距B点的水平距离为2
| R(H-R) |
点评:本题关键对两个的运动过程分析清楚,然后选择机械能守恒定律和平抛运动规律列式求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
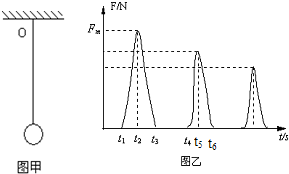 (2006?宿迁三模)利用传感器和计算机可以研究快速变化力的大小.实验时把图甲中的小球举到绳子的悬点O处,然后让小球自由下落.用这种方法获得的弹性绳的拉力随时间的变化的图象如图乙所示.根据图象所给的信息,以下判断正确的是( )
(2006?宿迁三模)利用传感器和计算机可以研究快速变化力的大小.实验时把图甲中的小球举到绳子的悬点O处,然后让小球自由下落.用这种方法获得的弹性绳的拉力随时间的变化的图象如图乙所示.根据图象所给的信息,以下判断正确的是( ) (2006?宿迁三模)用主尺最小分度为1mm,游标上有20个分度的卡尺测量一物体的长度,结果如图所示,可以读出此金属球的直径为
(2006?宿迁三模)用主尺最小分度为1mm,游标上有20个分度的卡尺测量一物体的长度,结果如图所示,可以读出此金属球的直径为 (2006?宿迁三模)地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴沿着一条与竖直方向成α角的直线MN运动.如图所示,由此可以判断( )
(2006?宿迁三模)地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴沿着一条与竖直方向成α角的直线MN运动.如图所示,由此可以判断( ) (2006?宿迁三模)汤姆生在测定阴极射线比荷时采用的方法是利用电场、磁场偏转法,即测出阴极射线在匀强电场或匀强磁场中穿过一定距离时的偏角.设竖直向下的匀强电场的电场强度为E,阴极射线垂直电场射入、穿过水平距离L后的运动偏角为θ(θ较小,θ≈tanθ)(如图A);以匀强磁场B代替电场,测出经过一段弧长L的运动偏角为φ(如图B),已知阴极射线入射的初速度相同,试以E、B、L、θ、φ表示阴极射线粒子的比荷q/m的关系式.(重力不计)
(2006?宿迁三模)汤姆生在测定阴极射线比荷时采用的方法是利用电场、磁场偏转法,即测出阴极射线在匀强电场或匀强磁场中穿过一定距离时的偏角.设竖直向下的匀强电场的电场强度为E,阴极射线垂直电场射入、穿过水平距离L后的运动偏角为θ(θ较小,θ≈tanθ)(如图A);以匀强磁场B代替电场,测出经过一段弧长L的运动偏角为φ(如图B),已知阴极射线入射的初速度相同,试以E、B、L、θ、φ表示阴极射线粒子的比荷q/m的关系式.(重力不计)