题目内容
 如图所示,光滑斜面末端与一个半径为R的光滑圆轨道平滑连接,两辆质量均为m的相同小车(大小可忽略),中间夹住一轻弹簧后用挂钩连接一起.两车从斜面上的某一高度由静止滑下,当两车刚滑入圆环最低点时连接两车的挂钩突然断开,弹簧将两车弹开,其中后车刚好停在圆环最低点处,前车沿圆环轨道运动恰能越过圆弧轨道最高点.已知重力加速度为g.求:
如图所示,光滑斜面末端与一个半径为R的光滑圆轨道平滑连接,两辆质量均为m的相同小车(大小可忽略),中间夹住一轻弹簧后用挂钩连接一起.两车从斜面上的某一高度由静止滑下,当两车刚滑入圆环最低点时连接两车的挂钩突然断开,弹簧将两车弹开,其中后车刚好停在圆环最低点处,前车沿圆环轨道运动恰能越过圆弧轨道最高点.已知重力加速度为g.求:(1)前车被弹出时的速度.
(2)两车下滑的高度h.
(3)把前车弹出过程中弹簧释放的弹性势能.
分析:(1)根据牛顿第二定律求出最高点的临界速度,再根据机械能守恒定律求出前车被弹出时的速度.
(2)根据动量守恒定律求出两车到达底端的速度,再根据机械能守恒定律求出下滑的高度.
(3)两车在最底端系统动能的增加等于弹簧释放的弹性势能,根据能量守恒定律求出弹簧释放的弹性势能.
(2)根据动量守恒定律求出两车到达底端的速度,再根据机械能守恒定律求出下滑的高度.
(3)两车在最底端系统动能的增加等于弹簧释放的弹性势能,根据能量守恒定律求出弹簧释放的弹性势能.
解答:解:(1)前车恰能越过圆轨道的最高点,它越过圆轨道最高点的速度为v0
根据mg=m
,解得v0=
.
前车被弹出时的速度为v1,根据机械能守恒定律得,
mv02+2mgR=
mv12
解得v1=
.
(2)设两车滑到圆轨道最低点时的速度为v,由动量守恒定律得,
mv1=2mv
解得v=
.
由机械能守恒定律得:
?2mv2=2mgh
解得h=
.
(3)把前车弹出时弹簧释放的弹性势能为:Ep=
mv12-
?2mv2=
mgR.
答:(1)前车被弹出时的速度为
.
(2)两车下滑的高度为
.
(3)把前车弹出过程中弹簧释放的弹性势能为
.
根据mg=m
| v02 |
| R |
| gR |
前车被弹出时的速度为v1,根据机械能守恒定律得,
| 1 |
| 2 |
| 1 |
| 2 |
解得v1=
| 5gR |
(2)设两车滑到圆轨道最低点时的速度为v,由动量守恒定律得,
mv1=2mv
解得v=
| ||
| 2 |
由机械能守恒定律得:
| 1 |
| 2 |
解得h=
| 5R |
| 8 |
(3)把前车弹出时弹簧释放的弹性势能为:Ep=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
答:(1)前车被弹出时的速度为
| 5gR |
(2)两车下滑的高度为
| 5R |
| 8 |
(3)把前车弹出过程中弹簧释放的弹性势能为
| 5mgR |
| 4 |
点评:本题综合考查了动量守恒定律、机械能守恒定律、能量守恒定律以及牛顿第二定律,对学生的综合能力要求较高,难度中等.

练习册系列答案
相关题目
 如图所示,光滑斜面的倾角为θ,若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出,问小球滑到斜面底端时水平位移s是多大?末速度vt多大?
如图所示,光滑斜面的倾角为θ,若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出,问小球滑到斜面底端时水平位移s是多大?末速度vt多大?

 ,s=vt,
,s=vt, .
.
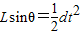 ,s=vt,
,s=vt, .
.