题目内容
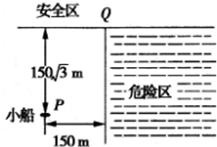2011年9月19日．一场百年未遇的洪水咆哮而至，大范围肆虐渠江广安沿岸，大学生村官李波带领大家进行抢险救灾工作．某一次营救受灾群众的小船到安全区的最近距离为15| 3 |
分析：根据题意，画出运动轨迹图，并结合力的平行四边形定则，即可求解．
解答：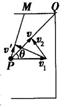
解：若小船刚好避开危险区，小船沿PQ方向以速度v行驶，
如图所示，v1为水流速度，
则小船在静水中的速度至少应为v2=v1sinθ．
显然小船沿其他方向如PM以速度v′行驶时在静水中的最小速度要大于v2，
又tanθ=
=
，
则小船在静水中的速度至少为v1sinθ=2
m/s．故B正确，ACD错误；
故选B
解：若小船刚好避开危险区，小船沿PQ方向以速度v行驶，如图所示，v1为水流速度，
则小船在静水中的速度至少应为v2=v1sinθ．
显然小船沿其他方向如PM以速度v′行驶时在静水中的最小速度要大于v2，
又tanθ=
150
| ||
| 150 |
| 3 |
则小船在静水中的速度至少为v1sinθ=2
| 3 |
故选B
点评：考查运动的合成与分解，掌握力的平行四边形定则，理解分运动与合运动的等时性．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
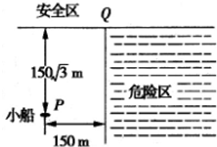
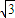m，从这里向下游150m处有一危险区，水流速度为4m/s，如图所示，为了使小船避开危险区沿直线到达对岸，小船在静水中的速度至少是（ ）
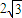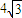/s
/s