Question

一根轻绳一端系一小球，另一端固定在O点，在O点有一个能测量绳的拉力大小的力传感器，让小球绕O点在竖直平面内做圆周运动，由传感器测出拉力F随时间t变化图象如图所示，已知小球在最低点A的速度v_A=6m/s，g=9.8m/s²取π²=g，求：
（1）小球做圆周运动的周期T；
（2）小球的质量m；
（3）轻绳的长度L．

Answer 1

分析：小球在竖直平面内做圆周运动，在最低点绳子的拉力和重力的合力提供向心力，此时拉力最大；在最高点，拉力和重力的合力提供向心力，此时拉力最小．根据图象求出求出小球的周期．根据牛顿第二定律与小球的机械能守恒定律，可列出方程求出小球的质量与轻绳的长度．

解答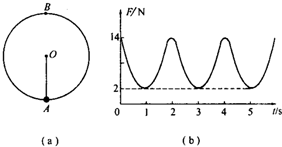：解：（1）由F与t的图象关系可知：小球圆周运动周期为2s
（2）当小球在最高点时，绳子的拉力最小；小球在最低点时，绳子的拉力最大．且小球从最低点到最高点过程中只有重力做功，所以小球的机械能守恒．
则有：最高点G+F₁═m

vA2

L

在最低点有：F2-G=m

vA2

R

根据机械能守恒定律得，

1

2

mvB2+mg?2R=

1

2

mvA2
联立三式解得m=0.2kg，L=0.6m．
答：（1）小球做圆周运动的周期为2s．
（2）小球的质量为0.2kg．
（3）轻绳的长度为0.6m．

点评：本题综合考查了牛顿第二定律、机械能守恒定律，知道圆周运动向心力的来源，确定何时拉力最大，何时拉力最小．