题目内容
16.验证小灯泡(可看成点光源)光能的球面散射规律并测定其发光效率,有同学设计并进行了如图1所示的实验:将一个“6V 8.0W”的小灯泡接入电路,使之正常发光,在灯泡灯丝的同一水平面、正对光线方向放一个测量光强的仪器,以测定与光源间距为d时相应的光强值I,共测得以下9组数据(见表).然后将表内数据分别在I-d,I-$\frac{1}{d}$和I-$\frac{1}{{d}^{2}}$坐标平面内作出如下数据点,如图2(a)(b)(c)所示.
| d/×10-2m | 6.50 | 7.50 | 8.50 | 9.50 | 10.5 | 11.5 | 12.5 | 13.5 | 14.5 |
| I/Wm-2 | 8.29 | 6.66 | 4.96 | 3.92 | 3.37 | 2.61 | 2.30 | 1.97 | 1.70 |
(2)在与光源等距的各点,认为光源向各方向发出的光强大小几乎相等.依点光源光能向周围空间360°球面均匀散射的物理模型,写出光源的发光功率P0、光强值I及相应的与光源距离d之间的关系式P0=4πd2I.(球面面积公式S=4πr2)
(3)根据以上条件,算出小电珠的电-光转换效率η=5.9%.
分析 (1)找出直线,直线表示横坐标与纵坐标成正比,然后求出斜率;
(2)光强等于单位时间流过单位面积的光能,相同时间内通过各个球面的能量是相等的;
(3)将光源的发光功率除以电功率,就可以得到发光效率.
解答 解:(1)图C为直线,故光强与距离的平方成正比;
表达式为:I=$\frac{k}{{d}^{2}}$,
斜率为:k≈0.0375W;
(2)光强等于单位时间流过单位面积的光能,故发光功率为:P0=SI=4πd2I;
(3)发光功率为:P0=SI=4πd2I=4×3.14×(13.5×0.01)2×1.97≈0.45W
发光效率:η=$\frac{0.45W}{8W}$×100%≈5.9%;
故答案为:(1)I=$\frac{k}{{d}^{2}}$;0.03.75W;(2)P0=4πd 2I;(3)5.9%.
点评 本题关键明确光强的物理意义以及其定义,同时要能结合图象进行分析计算.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7.下述做法能改善空气质量的是( )
| A. | 以煤等燃料作为主要生活燃料 | |
| B. | 利用太阳能、风能和氢能等能源替代化石能源 | |
| C. | 鼓励私人购买和使用汽车代替公交车 | |
| D. | 限制使用电动车 |
4. 如图所示,某同学用DIS设计了一个测物体瞬时速度的实验.
如图所示,某同学用DIS设计了一个测物体瞬时速度的实验.
第一次实验时,该同学在小车上固定挡光片时,使挡光片的前端朝向车头.依次更换四个挡光片,将小车从轨道上同一位置P由静止释放,获得了4组实验数据.第二次实验时,他将挡光片倒置,使挡光片的前端朝向车尾,仍将小车从轨道上同一位置P由静止释放,又得到了4组实验数据.实验完毕,得到两张表格.
表一
表二
分析表格中的数据,可知表一是将挡光片倒置后所得数据;四个挡光片中,最窄的挡光片的宽度△s=0.020m(结果保留到小数点后第三位);表中与小车车头到达光电门时的瞬时速度最接近的是0.342m/s.
 如图所示,某同学用DIS设计了一个测物体瞬时速度的实验.
如图所示,某同学用DIS设计了一个测物体瞬时速度的实验.第一次实验时,该同学在小车上固定挡光片时,使挡光片的前端朝向车头.依次更换四个挡光片,将小车从轨道上同一位置P由静止释放,获得了4组实验数据.第二次实验时,他将挡光片倒置,使挡光片的前端朝向车尾,仍将小车从轨道上同一位置P由静止释放,又得到了4组实验数据.实验完毕,得到两张表格.
表一
| 不同的挡光片 | 通过光电门的时间(s) | 速度(m/s) |
| A | 0.15425 | 0.519 |
| B | 0.11209 | 0.535 |
| C | 0.07255 | 0.551 |
| D | 0.03510 | 0.570 |
| 不同的挡光片 | 通过光电门的时间(s) | 速度(m/s) |
| A | 0.23048 | 0.349 |
| B | 0.17454 | 0.345 |
| C | 0.11562 | 0.344 |
| D | 0.05860 | 0.342 |
3. 如图所示,轻弹簧两端分别固定质量为ma、mb的小球a、b,通过两根细线将小球吊在水平天花板上.已知两球均处于静止状态,两细线与水平方向的夹角均为α,弹簧轴线沿水平方向,以下说法正确的是( )
如图所示,轻弹簧两端分别固定质量为ma、mb的小球a、b,通过两根细线将小球吊在水平天花板上.已知两球均处于静止状态,两细线与水平方向的夹角均为α,弹簧轴线沿水平方向,以下说法正确的是( )
 如图所示,轻弹簧两端分别固定质量为ma、mb的小球a、b,通过两根细线将小球吊在水平天花板上.已知两球均处于静止状态,两细线与水平方向的夹角均为α,弹簧轴线沿水平方向,以下说法正确的是( )
如图所示,轻弹簧两端分别固定质量为ma、mb的小球a、b,通过两根细线将小球吊在水平天花板上.已知两球均处于静止状态,两细线与水平方向的夹角均为α,弹簧轴线沿水平方向,以下说法正确的是( )| A. | a球所受细线的拉力大小为magsinα | |
| B. | a、b两球所受细线的拉力大小不一定相等 | |
| C. | b球所受弹簧的弹力的大小为mbgtanα | |
| D. | a、b两球的质量大小关系一定满足ma=mb |
7.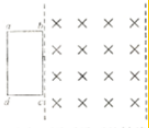 如图所示,空间存在宽度为3L、磁感应强度大小为B、方向垂直纸面向里的有界匀强磁场.均匀导线绕制的单匝矩形线框abcd,在纸面内从静止开始做加速度为a0的匀加速直线运动,速度方向垂直磁场边界向右.开始时,bc边紧挨着磁场左边界,运动中bc边与磁场边界平行.线框边长ab=L,bc=2L,其总电阻为R,则线框从进入到穿出磁场的过程中,下列说法正确的是( )
如图所示,空间存在宽度为3L、磁感应强度大小为B、方向垂直纸面向里的有界匀强磁场.均匀导线绕制的单匝矩形线框abcd,在纸面内从静止开始做加速度为a0的匀加速直线运动,速度方向垂直磁场边界向右.开始时,bc边紧挨着磁场左边界,运动中bc边与磁场边界平行.线框边长ab=L,bc=2L,其总电阻为R,则线框从进入到穿出磁场的过程中,下列说法正确的是( )
 如图所示,空间存在宽度为3L、磁感应强度大小为B、方向垂直纸面向里的有界匀强磁场.均匀导线绕制的单匝矩形线框abcd,在纸面内从静止开始做加速度为a0的匀加速直线运动,速度方向垂直磁场边界向右.开始时,bc边紧挨着磁场左边界,运动中bc边与磁场边界平行.线框边长ab=L,bc=2L,其总电阻为R,则线框从进入到穿出磁场的过程中,下列说法正确的是( )
如图所示,空间存在宽度为3L、磁感应强度大小为B、方向垂直纸面向里的有界匀强磁场.均匀导线绕制的单匝矩形线框abcd,在纸面内从静止开始做加速度为a0的匀加速直线运动,速度方向垂直磁场边界向右.开始时,bc边紧挨着磁场左边界,运动中bc边与磁场边界平行.线框边长ab=L,bc=2L,其总电阻为R,则线框从进入到穿出磁场的过程中,下列说法正确的是( )| A. | 流过线框截面的总电量为$\frac{4B{L}^{2}}{R}$ | |
| B. | 线框回路中始终有顺时针方向的感应电流 | |
| C. | ad边进入磁场前瞬间bc间的电势差为$\frac{2BL\sqrt{2{a}_{0}L}}{3}$ | |
| D. | ad边离开磁场前瞬间bc间的电势差为$\frac{4BL\sqrt{2{a}_{0}L}}{3}$ |




 如图是一种气压保温瓶的结构示意图.其中出水管很细,体积可忽略不计,出水管口与瓶胆口齐平,;用手按下按压器时,气室上方的小孔被堵塞,使瓶内气体压强增大,水在气压作用下从出水管口流出.最初瓶内水面低于水管口10cm,此时瓶内气体(含气室)的体积为2.0×102cm3,已知水的密度为1.0×103 kg/m3,按压器的自重不计,大气压P0=1.01×105 Pa,取g=10m/s2.求:
如图是一种气压保温瓶的结构示意图.其中出水管很细,体积可忽略不计,出水管口与瓶胆口齐平,;用手按下按压器时,气室上方的小孔被堵塞,使瓶内气体压强增大,水在气压作用下从出水管口流出.最初瓶内水面低于水管口10cm,此时瓶内气体(含气室)的体积为2.0×102cm3,已知水的密度为1.0×103 kg/m3,按压器的自重不计,大气压P0=1.01×105 Pa,取g=10m/s2.求: 半球形介质截面如图所示,O为圆心,相互平行的单色光a和b,从不同位置进入介质,光线a在O点恰好发生全反射.光线b的入射角为45°,求:
半球形介质截面如图所示,O为圆心,相互平行的单色光a和b,从不同位置进入介质,光线a在O点恰好发生全反射.光线b的入射角为45°,求: