题目内容
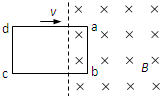 在光滑绝缘水平面上,一个电阻为0.1Ω、质量为0.05kg的矩形金属框abcd以10m/s的初速度滑进一匀强磁场,ab边长0.1m,如图所示为俯视图.匀强磁场的磁感应强度B为0.5T,方向竖直向下,范围足够大.当金属框有一部分滑进磁场,产生了1.6J的热量时,对金属框施加一垂直于ab边的水平外力,使它开始做匀减速运动(计为t=0时刻),第3s末使金属框的速度变为零,此时cd边仍在磁场外.则t=1s时,水平外力F的大小是
在光滑绝缘水平面上,一个电阻为0.1Ω、质量为0.05kg的矩形金属框abcd以10m/s的初速度滑进一匀强磁场,ab边长0.1m,如图所示为俯视图.匀强磁场的磁感应强度B为0.5T,方向竖直向下,范围足够大.当金属框有一部分滑进磁场,产生了1.6J的热量时,对金属框施加一垂直于ab边的水平外力,使它开始做匀减速运动(计为t=0时刻),第3s末使金属框的速度变为零,此时cd边仍在磁场外.则t=1s时,水平外力F的大小是分析:首先根据能量守恒求出金属框产生1.6J热量时的速度大小.此该以后线框做匀减速运动,由运动学公式可求得加速度,并能求出t=1s时的速度,根据安培力公式和牛顿第二定律求出外力F的大小.同理,确定出t=2s时外力F的方向.
解答:解:设金属框产生1.6J热量时的速度大小为v1,根据能量守恒定律得:
Q=
m
-
m
其中 m=0.05kg,v0=10m/s,Q=1.6J代入解得,v1=6m/s
设匀减速运动的加速度大小为a,由v1-at=0得
a=
=
=2m/s2
则t=1s时速度为v2=v1-at=6-2×1=4m/s
设此时外力F的大小为F,方向水平向右,则有
-F=ma
解得,F=0
t=2s时速度为v3=v1-at=6-2×2=2m/s
设此时外力F的大小为F′,方向水平向右,则有
-F′=ma
解得,F′=-0.05N,说明外力F方向水平向左.
故答案为:0,水平向左
Q=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
其中 m=0.05kg,v0=10m/s,Q=1.6J代入解得,v1=6m/s
设匀减速运动的加速度大小为a,由v1-at=0得
a=
| v1 |
| t |
| 6 |
| 3 |
则t=1s时速度为v2=v1-at=6-2×1=4m/s
设此时外力F的大小为F,方向水平向右,则有
| B2L2v2 |
| R |
解得,F=0
t=2s时速度为v3=v1-at=6-2×2=2m/s
设此时外力F的大小为F′,方向水平向右,则有
| B2L2v3 |
| R |
解得,F′=-0.05N,说明外力F方向水平向左.
故答案为:0,水平向左
点评:本题是能量守恒定律、牛顿第二定律和运动学公式的综合应用,要掌握安培力的表达式F=
,采用假设法求解.
| B2L2v |
| R |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
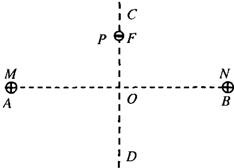 如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )
如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(设不改变原来的电场分布),在以后的一段时间内,P在CD连线上做往复运动.若( )| A、小球P的带电量缓慢减小,则它往复运动过程中振幅不断减小 | B、小球P的带电量缓慢减小,则它往复运动过程中每次经过O点时的速率不断减小 | C、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中周期不断减小 | D、点电荷M、N的带电量同时等量地缓慢增大,则小球P往复运动过程中振幅不断减小 |
 如图所示,在光滑绝缘水平面上有一正方形线框abcd,线框由均匀电阻丝制成,边长为L,总电阻值为R.两条平行虚线之间存在匀强磁场,磁感应强度为B,磁场方向竖直向上.线框在水平拉力F的作用下,沿水平面以速度v0匀速进入磁场区域,在运动过程中,线框ab、cd两边始终与磁场边界平行.
如图所示,在光滑绝缘水平面上有一正方形线框abcd,线框由均匀电阻丝制成,边长为L,总电阻值为R.两条平行虚线之间存在匀强磁场,磁感应强度为B,磁场方向竖直向上.线框在水平拉力F的作用下,沿水平面以速度v0匀速进入磁场区域,在运动过程中,线框ab、cd两边始终与磁场边界平行. 如图所示,在光滑绝缘水平面上,有两个大小相同、可视为质点的小球沿同一直线相向运动,A球带电荷量+2Q、质量为m,B球带电荷量+Q、质量为2m.当它们相距L时,它们的速度大小恰好相等,此时A的加速度为a;当B的加速度也为a时,某一球的速度为零,最终两球没有相碰.则以下判断正确的是( )
如图所示,在光滑绝缘水平面上,有两个大小相同、可视为质点的小球沿同一直线相向运动,A球带电荷量+2Q、质量为m,B球带电荷量+Q、质量为2m.当它们相距L时,它们的速度大小恰好相等,此时A的加速度为a;当B的加速度也为a时,某一球的速度为零,最终两球没有相碰.则以下判断正确的是( )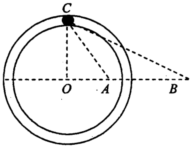 如图所示,在光滑绝缘水平面上固定着-根光滑绝缘的圆形水平渭槽,其圆心在O点.过O点的-条直径上的A、B两点固定着两个点电荷.其中固定于A点的为正电荷,电荷量大小为Q;固定于B点的是未知电荷.在它们形成的电场中,有-个可视为质点的质量为m、电荷量大小为q的带电小球正在滑槽中运动,小球的速度方向平行于水平面,若已知小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度,AB间的距离为L,∠ABC=∠ACB=30°,CO⊥OB,静电力常量为k,
如图所示,在光滑绝缘水平面上固定着-根光滑绝缘的圆形水平渭槽,其圆心在O点.过O点的-条直径上的A、B两点固定着两个点电荷.其中固定于A点的为正电荷,电荷量大小为Q;固定于B点的是未知电荷.在它们形成的电场中,有-个可视为质点的质量为m、电荷量大小为q的带电小球正在滑槽中运动,小球的速度方向平行于水平面,若已知小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度,AB间的距离为L,∠ABC=∠ACB=30°,CO⊥OB,静电力常量为k, 如图所示,在光滑绝缘水平面上,有一个质量为m,带电量为+Q 的带电体,其右侧一段距离处有一根轻质绝缘的弹簧,弹簧右端固定,左端O自由.现在水平面上方加一水平向右的匀强电场E,使带电体在电场力作用下向右运动,已知弹簧的最大压缩量为X0,则关于带电体的加速度a 的大小与弹簧的压缩量X 的关系,下列图象正确的是( )
如图所示,在光滑绝缘水平面上,有一个质量为m,带电量为+Q 的带电体,其右侧一段距离处有一根轻质绝缘的弹簧,弹簧右端固定,左端O自由.现在水平面上方加一水平向右的匀强电场E,使带电体在电场力作用下向右运动,已知弹簧的最大压缩量为X0,则关于带电体的加速度a 的大小与弹簧的压缩量X 的关系,下列图象正确的是( )


