题目内容
19.一质点由静止开始从A点向B点作直线运动,初始加速度为a0(1)若以后加速度均匀增加,每经过n秒增加a0,求经过t秒后质点的速度.
(2)若将质点的位移SAB平分为n等份,且每过一个等分点后,加速度都增加$\frac{{a}_{0}}{n}$,求该质点到达B点时的速度.
分析 (1)作出质点的加速度随时间的图线,结合图线围成的面积求出速度的变化量,从而得出t秒后质点的速度.
(2)将质点的位移SAB平分为n等份,得出每一等份内的加速度,结合速度位移公式对每一段列出方程,通过累计计算求出质点到达B点的速度大小.
解答 解:(1)作出a-t图线,图线围成的面积表示速度的变化量,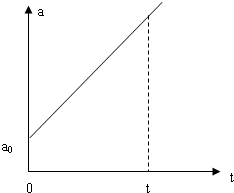
每经过n秒增加a0,则ts时,加速度a=${a}_{0}+\frac{t}{n}{a}_{0}$,
则ts内速度的变化量$△v=\frac{1}{2}({a}_{0}+{a}_{0}+\frac{t}{n}{a}_{0})t$=${a}_{0}t+\frac{{a}_{0}}{2n}{t}^{2}$.
因为初速度为零,则ts后的速度v=${a}_{0}t+\frac{{a}_{0}}{2n}{t}^{2}$.
(2)根据速度位移公式得,$2{a}_{0}\frac{{s}_{AB}}{n}={{v}_{1}}^{2}-0$,
$2({a}_{0}+\frac{{a}_{0}}{n})\frac{{s}_{AB}}{n}={{v}_{2}}^{2}-{{v}_{1}}^{2}$.
$2({a}_{0}+\frac{(n-1){a}_{0}}{n})\frac{{s}_{AB}}{n}={{v}_{B}}^{2}-{{v}_{n-1}}^{2}$.
累加,解得${v}_{B}=\sqrt{(3-\frac{1}{n})a{s}_{AB}}$.
答:(1)经过t秒后质点的速度为${a}_{0}t+\frac{{a}_{0}}{2n}{t}^{2}$.
(2)该质点到达B点时的速度为$\sqrt{(3-\frac{1}{n})a{s}_{AB}}$.
点评 解决本题的关键知道a-t图线围成的面积表示速度的变化量,对于第二问,对数学要求的能力要求较高,通过速度位移公式,累计计算进行求解.

| A. | 1N/m | B. | 10N/m | C. | 100N/m | D. | 1000N/m |

| A. | 甲是α-t | B. | 乙是s-t | C. | 丙是v-t | D. | 丁是α-t |
| A. | EA=EB之点,只有一处,该处合场强为0 | |
| B. | EA=EB之点有两处,一处合场强为0,另一处合场强为2EA | |
| C. | EA=EB之点共有三处,其中两处合场强为0;另一处合场强为2EA | |
| D. | EA=EB之点共有三处,其中一处合场强为0,另二处合场强为2EA |
 如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )
如图所示,在a点由静止释放一个质量为m、电荷量为+q的带电粒子,粒子到达b点时速度恰好为零,设ab所在的电场线为竖直方向,a、b间的高度差为h,则( )| A. | ab所在电场线方向为竖直向上 | |
| B. | 带电粒子从a点运动到b点过程中电场力做功为零 | |
| C. | a、b两点间的电势差Uab=-$\frac{mgh}{q}$ | |
| D. | b点场强大于a点场强 |
| A. | 物体经A点的速度大小为$\frac{{x}_{1}+{x}_{2}}{2T}$ | |
| B. | 物体运动的加速度为$\frac{{x}_{1}+{x}_{2}}{{T}^{2}}$ | |
| C. | 物体到达B点的速度大小为 $\frac{{x}_{1}+{x}_{2}}{T}$ | |
| D. | 物体运动的加速度为$\frac{{x}_{2}-{x}_{1}}{{T}^{2}}$ |
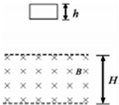 如图所示,以刚性矩形铜质线圈从某一高处自由下落,进入一个水平的有界匀强磁场区域,然后穿出磁场区域.竖直方向上线圈的长度h小于磁场的长度H,运动过程中线圈平面始终在竖直平面内且不发生转动.下列P-x图线能定性表示线圈在通过磁场过程由感应电流的功率P随下落位移x变化的是( )
如图所示,以刚性矩形铜质线圈从某一高处自由下落,进入一个水平的有界匀强磁场区域,然后穿出磁场区域.竖直方向上线圈的长度h小于磁场的长度H,运动过程中线圈平面始终在竖直平面内且不发生转动.下列P-x图线能定性表示线圈在通过磁场过程由感应电流的功率P随下落位移x变化的是( )



 如图所示,一个重为5N的物体静止在倾斜角为30°的粗糙斜面上,该物体受到沿斜面向上的3N的摩擦力和4N的支持力,则:
如图所示,一个重为5N的物体静止在倾斜角为30°的粗糙斜面上,该物体受到沿斜面向上的3N的摩擦力和4N的支持力,则: