题目内容
(8分)如图所示,一不透明的圆柱形容器内装满折射率n= 的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成450角放置,若容器高为2 dm,底边半径为(1+
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成450角放置,若容器高为2 dm,底边半径为(1+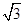 )dm,OM=1 dm,在容器中央正上方1 dm 处水平放置一足够长的刻度尺,
)dm,OM=1 dm,在容器中央正上方1 dm 处水平放置一足够长的刻度尺,
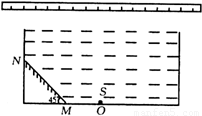
求光源S发出的光线经平面镜反射后,照射到刻度尺的长度.(不考虑容器侧壁和液面的反射)
【答案】
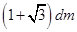
【解析】
试题分析:作出边界光路.当光线沿OM入射到平面镜时,发生反射,光线照射到刻度尺的最右端.当射到平面镜上的光线经折射照射到刻度尺的最左端时,根据对称性,作出平面镜反射的光路.
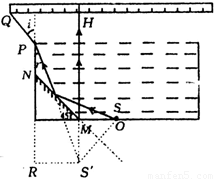
作图找出发光点S在平面镜中的像点S//,连接S/M延长交直尺于H点,由题设知:光线SM的入射角为45°,根据反射定律可知反射角等于45°,MH沿竖直方向,连接S/P,根据对称性得 S/M=OM=1m,在RtΔPRS//中,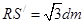 ,
,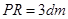 ,
,
由几何知识得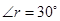
由折射定律可得: 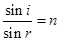
解得: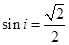 ,
,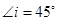
故刻度尺上被照亮的范围为: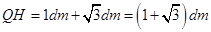
考点:本题考查对光的反射定律与光的折射定律的理解和应用,同时考查考生的理解能力、推理能力和分析综合能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
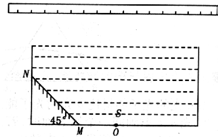 (2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n=
(2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n= 的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+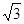 )dm,OM = 1dm,在容器中央正上方1
dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度。(不考虑容器侧壁和液面的反射)
)dm,OM = 1dm,在容器中央正上方1
dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度。(不考虑容器侧壁和液面的反射)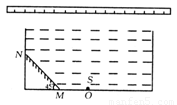

 的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+
的透明液体,容器底部正中央O点处有一点光源S,平面镜MN与底面成45°角放置,若容器高为2dm,底边半径为(1+ )dm,OM = 1dm,在O点正上方离容器底部3 dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度。(不考虑容器侧壁和液面的反射)
)dm,OM = 1dm,在O点正上方离容器底部3 dm 处水平放置一足够长的刻度尺,求光源 S 发出的光线经平面镜反射后,照射到刻度尺的长度。(不考虑容器侧壁和液面的反射)