题目内容
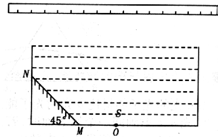 (2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n=
(2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n=| 2 |
| 3 |
分析:作出边界光路.当光线沿OM入射到平面镜时,发生反射,光线照射到刻度尺的最右端.当射到平面镜上的光线经折射照射到刻度尺的最左端时,根据对称性,作出平面镜反射的光路.根据反射定律和折射定律以及几何知识求解光线经平面镜反射后,照射到刻度尺的长度.
解答:解:设容器高为H.作图找出发光点S在平面镜中的像点S′,连接SM延长交直尺于H点.
由题:光线SM的入射角为45°,根据反射定律可知反射角等于45°,则MH沿竖直方向.
连接S′P,根据对称性得 S′M=OM=1m,则在Rt△PR S′中,R S′=
dm,PR=H+S′M=3dm
由几何知识得∠r=30°.
根据折射定律可得:n=
解得sini=
,∠i=45°,
故刻度尺上被照亮的范围QH=1dm+
dm=(1+
)dm
答:刻度尺上被照亮的范围QH=1dm+
dm=(1+
)dm.
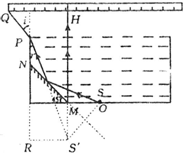
由题:光线SM的入射角为45°,根据反射定律可知反射角等于45°,则MH沿竖直方向.
连接S′P,根据对称性得 S′M=OM=1m,则在Rt△PR S′中,R S′=
| 3 |
由几何知识得∠r=30°.
根据折射定律可得:n=
| sini |
| sinr |
解得sini=
| ||
| 2 |
故刻度尺上被照亮的范围QH=1dm+
| 3 |
| 3 |
答:刻度尺上被照亮的范围QH=1dm+
| 3 |
| 3 |

点评:对于范围问题,往往要作出边界光线,研究临界情况,利用几何知识和折射定律、反射定律结合研究,这是常用的思路.

练习册系列答案
相关题目
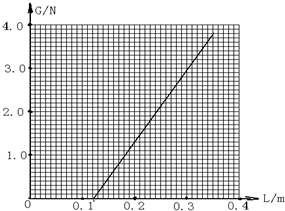 (2011?咸阳三模)某研究小组在“探究弹力和弹簧伸长关系”的实验中,将不同数量的钩碼挂在竖直弹簧下端进行测量,根据实验数据,利用描点法作出钩碼的重力G与弹簧的总长L的关系图象,如图所示
(2011?咸阳三模)某研究小组在“探究弹力和弹簧伸长关系”的实验中,将不同数量的钩碼挂在竖直弹簧下端进行测量,根据实验数据,利用描点法作出钩碼的重力G与弹簧的总长L的关系图象,如图所示 (2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )
(2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )