题目内容
1.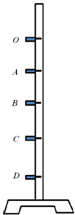 如图为验证小球做自由落体运动时机械能守恒的装置图.图中O点为释放小球的初始位置,A、B、C、D各点为固定速度传感器的位置,A、B、C、D、O各点在同一竖直线上.
如图为验证小球做自由落体运动时机械能守恒的装置图.图中O点为释放小球的初始位置,A、B、C、D各点为固定速度传感器的位置,A、B、C、D、O各点在同一竖直线上.(1)已知当地重力加速度为g,要完成实验,必须要测量的物理量是BC;
A.小球的质量m
B.小球下落到每一个速度传感器时的速度v
C.各速度传感器与O点之间的竖直距离h
D.小球自初始位置至下落到每一个速度传感器时所用的时间t
(2)作出v2h图象,由图象算出其斜率k,当k=2g时,可以认为小球在下落过程中系统机械能守恒;
(3)经正确操作,发现小球动能增加量$\frac{1}{2}$mv2总是稍小于重力势能减小量mgh,请写出对减小本实验误差有益的一条建议:为减小测量的相对误差,建议相邻速度传感器间的距离适当大些,或为减小空气阻力的影响,建议选用质量大、体积小的球做实验等.
分析 (1)根据需要验证的方程:mgh=$\frac{1}{2}$mv2,确定需要测量的物理量.
(2)根据mgh=$\frac{1}{2}$mv2,得到v2与h的关系式,分析v2-h图象斜率的物理意义.
(3)要减小实验误差,测量的量应相对大些,选用质量大、体积小的球做实验等.
解答 解:(1)小球做自由落体运动时,由机械能守恒定律得:mgh=$\frac{1}{2}$mv2,即gh=$\frac{1}{2}$v2,故需要测量小球下落到每一个速度传感器时的速度v和高度h,不需要测量小球的质量m和下落时间时间t.故BC正确,AD错误.
(2)由mgh=$\frac{1}{2}$mv2,得v2=2gh,则v2-h图象的斜率k=2g.
(3)为了减小测量的相对误差,建议相邻速度传感器间的距离适当大些;为减小空气阻力的影响,建议选用质量大、体积小的球做实验等.
故答案为:(1)BC;(2)2g;(3)为减小测量的相对误差,建议相邻速度传感器间的距离适当大些;或为减小空气阻力的影响,建议选用质量大、体积小的球做实验等.
点评 本实验以小球做自由落体运动为例,验证机械能守恒定律,根据方程mgh=$\frac{1}{2}$mv2,分析v2-h图象斜率的意义是常用的方法.

练习册系列答案
相关题目
11.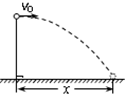 如图所示,将一个小球从某一高度处以初速度v0水平抛出,小球经时间t落地,落地前瞬间重力的功率为P.不计空气阻力.若将小球从相同位置以2v0的速度水平抛出,则小球( )
如图所示,将一个小球从某一高度处以初速度v0水平抛出,小球经时间t落地,落地前瞬间重力的功率为P.不计空气阻力.若将小球从相同位置以2v0的速度水平抛出,则小球( )
 如图所示,将一个小球从某一高度处以初速度v0水平抛出,小球经时间t落地,落地前瞬间重力的功率为P.不计空气阻力.若将小球从相同位置以2v0的速度水平抛出,则小球( )
如图所示,将一个小球从某一高度处以初速度v0水平抛出,小球经时间t落地,落地前瞬间重力的功率为P.不计空气阻力.若将小球从相同位置以2v0的速度水平抛出,则小球( )| A. | 落地的时间仍为t | B. | 落地的时间变为$\frac{t}{2}$ | ||
| C. | 落地前瞬间重力的功率仍为P | D. | 落地前瞬间重力的功率变为2P |
9. 如图,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B,则( )
如图,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B,则( )
 如图,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B,则( )
如图,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B,则( )| A. | B对A的压力大小为$\frac{R+r}{R}$mg | B. | A对地面的摩擦力方向向左 | ||
| C. | 细线对小球的拉力大小为$\frac{r}{R}$mg | D. | A对地面的压力等于Mg |
16. 如图所示,相同的乒乓球1、2恰好在等高处水平越过球网,不计乒乓球的旋转和空气阻力,乒乓球自最高点到落台的过程中,正确的是( )
如图所示,相同的乒乓球1、2恰好在等高处水平越过球网,不计乒乓球的旋转和空气阻力,乒乓球自最高点到落台的过程中,正确的是( )
 如图所示,相同的乒乓球1、2恰好在等高处水平越过球网,不计乒乓球的旋转和空气阻力,乒乓球自最高点到落台的过程中,正确的是( )
如图所示,相同的乒乓球1、2恰好在等高处水平越过球网,不计乒乓球的旋转和空气阻力,乒乓球自最高点到落台的过程中,正确的是( )| A. | 过网时球1的速度小于球2的速度 | |
| B. | 球1的飞行时间大于球2的飞行时间 | |
| C. | 球1的速度变化率等于球2的速度变化率 | |
| D. | 落台时,球1的速率大于球2的速率 |
6.万有引力定律揭示了自然界中物体间一种基本相互作用规律.下列说法正确的是( )
| A. | 牛顿不仅提出了万有引力定律,并较为精确的测出了引力常量 | |
| B. | 人造地球卫星绕地球的向心力由地球对它的万有引力提供 | |
| C. | 万有引力定律只适用于天体,不适用于地面上的物体 | |
| D. | 宇宙飞船内的宇航员处于失重状态是由于没有受到万有引力的作用 |
13.寻找马航失联客机时,初步确定失事地点位于南纬31°52′东经115°52′的澳大利亚西南城市珀斯附近的海域,有一颗绕地球做匀速圆周运动的卫星,每天上午同一时刻在该区域的正上方海面照像.已知地球半径为R,地表重力加速度为g,卫星轨道半径为r.下列说法正确的是( )
| A. | 该卫星的运行速度大于第一宇宙速度 | |
| B. | 该卫星可能是同步卫星 | |
| C. | 该卫星的向心加速度为$\frac{{R}^{2}}{{r}^{2}}$g | |
| D. | 该卫星的周期为T=$\sqrt{\frac{4{π}^{2}r}{g}}$ |
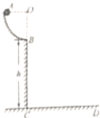 如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑$\frac{1}{4}$圆形轨道,B点距地面高为h=0.8m,C点处在B点正下方,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑,经B点飞出落到水平轨道上的D点(g取10m/s2)
如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑$\frac{1}{4}$圆形轨道,B点距地面高为h=0.8m,C点处在B点正下方,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑,经B点飞出落到水平轨道上的D点(g取10m/s2)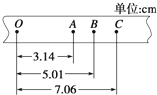 在“验证机械能守恒定律”的实验中,打点周期为0.02s,自由下落的重物质量为1kg,打出一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有多个点没画出,打点计时器打下点B时,物体的速度vB=0.98m/s,从起点O到打下B点的过程中,重力势能的减少量△Ep=0.49J,此过程中物体动能的增量△Ek=0.48J.(答案保留两位有效数字)
在“验证机械能守恒定律”的实验中,打点周期为0.02s,自由下落的重物质量为1kg,打出一条理想的纸带,数据如图所示,单位是cm,g取9.8m/s2,O、A之间有多个点没画出,打点计时器打下点B时,物体的速度vB=0.98m/s,从起点O到打下B点的过程中,重力势能的减少量△Ep=0.49J,此过程中物体动能的增量△Ek=0.48J.(答案保留两位有效数字)