题目内容
【题目】如图所示，用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内，其弯曲部分是由两个半径均为R=0.2m的半圆平滑对接而成（圆的半径远大于细管内径），轨道底端D点与水平地面相切。现一辆质量为m=0.1kg的玩具小车，在恒定功率P=1W的牵引力作用下加速到D点关闭发动机后进入“S”形轨道，从轨道的最高点A飞出后，恰好垂直撞在固定斜面B上的C点，C点与下半圆的圆心等高，已知：斜面的倾角为θ=30，假设小车在整个运动过程中的阻力不计。求:
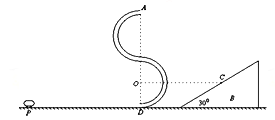
(1)小车离开A点瞬间的速度大小
(2)在A点小车对轨道的压力的大小和方向
(3)小车在水平地面的运动时间t
【答案】（1）
（2）mg 方向竖直向上 （3）1s
【解析】试题分析：小车离开A后做平抛运动，根据竖直方向的分运动可以求出小车的运动时间与竖直分速度，然后在C点根据运动的合成与分解可以求出小车的速度；小车在A点做圆周运动，由牛顿第二定律求出求出轨道对小车的支持力，然后由牛顿第三定律求出小车对轨道的压力；根据动能定理求出运动时间。
（1）把C点的速度分解为水平vA和竖直的vy，有： 
，
竖直速度为： 
，
竖直方向有： 
， 
解得小车在A点的速度大小： 
（2）因为
，对外轨有压力，轨道对小车的作用力向下，
由向心力公式得： 
,
解得: 
=1N
根据牛顿第三定律，小车对轨道的压力： 
=1N，方向竖直向上
(3)从P到A运用动能定理: 
代入数据解得： t=1s
练习册系列答案
相关题目
