题目内容
一个质量m=20kg的钢件，架在两根完全相同的、平行的长直圆柱上，如图所示，钢件的重心与两柱等距，两柱的轴线在同一水平面内，圆柱的半径r=0.025m，钢件与圆柱间的滑动摩擦系数μ=0.20，两圆柱各绕自己的轴线做转向相反的转动，角速度ω=40rad/s，若沿平行于柱轴方向施加力推着钢件做速度为v0=0.05m/s的匀速运动，推力是多大？设钢件左右受光滑槽限制（图中未画出），不发生横向运动．g取10m/s2．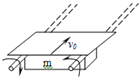
每根圆柱所受的压力均等于
，所以每根圆柱对钢件的滑动摩擦力f=
=20N．f的方向，应该跟圆柱钢件的接触部分，相对于钢件的速度方向相同．
以钢件为参照物，圆柱与钢件接触的部分，一方面有沿圆柱轴线的速度，大小v1=0.05m/s，另一方面有垂直于圆柱轴线方向的速度，大小为v2=rω=1m/s．
所以圆柱与钢件接触部分的速度与轴线方向的夹角θ满足
cotθ=
=0.05 因为v1＜＜v2，所以cosθ≈cotθ=0.05
而f与轴线之间的夹角也为θ
根据力的平衡，F=2fcosθ=2×20×0.05=2N．
| mg |
| 2 |
| μmg |
| 2 |
以钢件为参照物，圆柱与钢件接触的部分，一方面有沿圆柱轴线的速度，大小v1=0.05m/s，另一方面有垂直于圆柱轴线方向的速度，大小为v2=rω=1m/s．
所以圆柱与钢件接触部分的速度与轴线方向的夹角θ满足
cotθ=
| v1 |
| v2 |
而f与轴线之间的夹角也为θ
根据力的平衡，F=2fcosθ=2×20×0.05=2N．
练习册系列答案
相关题目
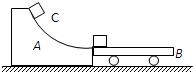（2013?永州一模）如右图所示，A为有光滑曲面的固定轨道，轨道底端的切线方向是水平的．质量M=40kg的小车B静止于轨道右侧，其上表面与轨道底端在同一水平面上．一个质量m=20kg的物体C以2.0m/s的初速度从轨道顶端滑下，冲上小车B后经一段时间与小车相对静止并一起运动．若轨道顶端与底端的高度差h=1.6m．物体与小车板面间的动摩擦因数μ=0.40，小车与水平面间的摩擦忽略不计．（取g=10m/s2），求：
如图所示，一个质量m=20kg的物块，在F=60N的水平拉力作用下，从静止开始沿水平地面向右做匀加速直线运动．物块与地面间的动摩擦因数?=0.10．取重力加速度g=10m/s2．
如图所示，一个质量m=20kg的物体放在光滑水平地面上．对物体施加一个F=10N的水平拉力，使物体由静止开始做匀加速直线运动．求：