题目内容
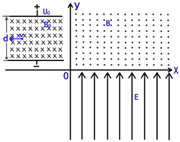
【题目】如图,真空中有一速度选择器,平行金属板上板接电源正极,下板接电源负极,板间电压为U0,板间距离为d,板间内垂直纸面向内的匀强磁场磁感应强度为B0,在直角坐标系第一象限有磁感应强度为B方向垂直纸面向外的匀强磁场,第四象限为电场强度为E方向竖直向上的匀强电场,有一质量为m,电荷量为q(重力不计)带正电的粒子匀速通过速度选择器后垂直进入第一象限磁场,经第一象限磁场再垂直X轴进入第四象限电场,求:
(1)粒子进入第一象限磁场的速度;
(2)粒子第三次经过X轴时的坐标;
(3)粒子从进入第一象限到第三次经过X轴运动的总时间。
【答案】(1)![]() ;(2)(
;(2)(![]() ,0);(3)
,0);(3)![]() ;
;
【解析】(1)在受到选择器中,由平衡条件得:
qvB0= ![]() ,解得,粒子速度:
,解得,粒子速度: ![]() ;
;
(2)粒子在磁场中做匀速圆周运动洛伦兹力提供向心力,
由牛顿第二定律得:qvB= ![]() ,解得:r=
,解得:r=![]() ,
,
粒子第三次经过x轴时的坐标:X=r+2r=![]() ;
;
(3)粒子第一次在磁场转过1/4圆周,第二次转过1/2圆周,
转过的总圆心角:θ=![]() ,粒子在磁场做圆周运动的周期:T=
,粒子在磁场做圆周运动的周期:T=![]() ,
,
粒子在磁场中的运动时间:t=![]() ;
;

练习册系列答案
相关题目