题目内容
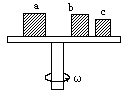
如图所示,一水平平台可绕竖直轴转动,平台上有a、b、c三个物体,其质量之比ma:mb:mc=2:1:1,它们到转轴的距离之比ra:rb:rc=1:1:2,三物块与平台间的动摩擦因数相同,且最大静摩擦力均与其压力成正比,当平台转动的角速度逐渐增大时,物块将会产生滑动,以下判断正确的是( )
A.a先滑
B.b先滑
C.c先滑
D.a、c同时滑
【答案】分析:A、B、C三个物体放在匀速转动的水平转台上,随转台做匀速圆周运动,由静摩擦力提供向心力,根据牛顿第二定律分析物体受到的静摩擦力大小.当物体所受的静摩擦力达到最大值时开始滑动.根据产生离心运动的条件分析哪个物体先滑动.
解答:解:
a、b、c三个物体的角速度相同,设角速度为ω,则三个物体受到的静摩擦力分别为
fA=mAω2rA,
fB=mBω2rB= mAω2rA,
mAω2rA,
fC=mCω2rC= mAω2?2rA=mAω2rA.
mAω2?2rA=mAω2rA.
所以物体a受到的摩擦力最大,物体b受到的摩擦力最小.
根据向心加速度a=ω2r,ω相同,c的半径r最大,则物体c的向心加速度最大.
三个物体受到的最大静摩擦力分别为:
fAm=μmAg,
fBm=μmBg= μmAg,
μmAg,
fCm=μmCg= μmAg.
μmAg.
转台转速加快时,角速度ω增大,三个受到的静摩擦力都增大,物体c的静摩擦力先达到最大值,最先滑动起来.故C正确,ABD错误.
故选C
点评:本题比较静摩擦力和向心加速度时要抓住三个物体的角速度相等.
解答:解:
a、b、c三个物体的角速度相同,设角速度为ω,则三个物体受到的静摩擦力分别为
fA=mAω2rA,
fB=mBω2rB=
 mAω2rA,
mAω2rA,fC=mCω2rC=
 mAω2?2rA=mAω2rA.
mAω2?2rA=mAω2rA.所以物体a受到的摩擦力最大,物体b受到的摩擦力最小.
根据向心加速度a=ω2r,ω相同,c的半径r最大,则物体c的向心加速度最大.
三个物体受到的最大静摩擦力分别为:
fAm=μmAg,
fBm=μmBg=
 μmAg,
μmAg,fCm=μmCg=
 μmAg.
μmAg.转台转速加快时,角速度ω增大,三个受到的静摩擦力都增大,物体c的静摩擦力先达到最大值,最先滑动起来.故C正确,ABD错误.
故选C
点评:本题比较静摩擦力和向心加速度时要抓住三个物体的角速度相等.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
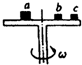 如图所示,一水平平台可绕竖直轴转动,平台上有a、b、c三个物体,其质量之比ma:mb:mc=2:1:1,它们到转轴的距离之比ra:rb:rc=1:1:2,三物块与平台间的动摩擦因数相同,且最大静摩擦力均与其压力成正比,当平台转动的角速度逐渐增大时,物块将会产生滑动,以下判断正确的是( )
如图所示,一水平平台可绕竖直轴转动,平台上有a、b、c三个物体,其质量之比ma:mb:mc=2:1:1,它们到转轴的距离之比ra:rb:rc=1:1:2,三物块与平台间的动摩擦因数相同,且最大静摩擦力均与其压力成正比,当平台转动的角速度逐渐增大时,物块将会产生滑动,以下判断正确的是( )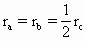 ,与平台间的最大静摩擦力均与其正压力成正比.将平台转动的角速度逐渐增大时
,与平台间的最大静摩擦力均与其正压力成正比.将平台转动的角速度逐渐增大时