题目内容
4.“嫦娥三号”探月卫星计划于2013年在西昌卫星发射中心发射升空.若该卫星在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径为R2,地球表面处的重力加速度为g,则( )| A. | 月球表面处的重力加速度为$\frac{G_2}{G_1}$g | |
| B. | 卫星在月球表面轨道上做匀速圆周运动的周期为2π$\sqrt{\frac{{{R_2}{G_1}}}{{g{G_2}}}}$ | |
| C. | 月球的质量与地球的质量之比为$\frac{{{G_1}R_2^2}}{{{G_2}R_1^2}}$ | |
| D. | 月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{{G_2}{R_2}}}{{{G_1}{R_1}}}}$ |
分析 根据重力表达式G=mg表示出g进行比较,
忽略星球自转的影响,根据万有引力等于重力列出等式.
研究卫星在月球表面轨道上做匀速圆周运动,根据万有引力提供向心力,列出等式求解.
第一宇宙速度是近地卫星的环绕速度,也是最大的圆周运动的环绕速度.
解答 解:A、该卫星在地球表面的重力为G1,在月球表面的重力为G2,
地球表面处的重力加速度为g,
根据重力表达式G=mg得:月球表面处的重力加速度为$\frac{G_2}{G_1}$g.故A正确.
B、研究卫星在月球表面轨道上做匀速圆周运动,根据万有引力提供向心力,列出等式
$\frac{GMm}{{R}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$R
T=2π$\sqrt{\frac{{R}^{3}}{GM}}$,
忽略星球自转的影响,根据万有引力等于重力列出等式
$\frac{GMm}{{R}^{2}}$=mg
M=$\frac{{gR}^{2}}{G}$
所以卫星在月球表面轨道上做匀速圆周运动的周期为2π$\sqrt{\frac{{{R_2}{G_1}}}{{g{G_2}}}}$,故B正确.
C、根据M=$\frac{{gR}^{2}}{G}$,
月球的质量与地球的质量之比是$\frac{{G}_{2}{R}_{2}^{2}}{{G}_{1}{R}_{1}^{2}}$,故C错误;
D、根据第一宇宙速度定义得
v=$\sqrt{\frac{GM}{R}}$=$\sqrt{gR}$
所以月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{{G_2}{R_2}}}{{{G_1}{R_1}}}}$,故D正确.
故选:ABD.
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案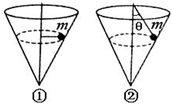 在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内作水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图①中小环与小球在同一水平面上,图②中轻绳与竖直轴成θ角.设①图和②图中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内作水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图①中小环与小球在同一水平面上,图②中轻绳与竖直轴成θ角.设①图和②图中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )| A. | Ta一定为零,Tb一定为零 | B. | Ta可以为零,Tb可以不为零 | ||
| C. | Na一定不为零,Nb不可以为零 | D. | Na可以为零,Nb可以不为零 |
 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为Ff,当轻绳与水平面的夹角为θ时,船的速度为v,人的拉力大小为F,则此时( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为Ff,当轻绳与水平面的夹角为θ时,船的速度为v,人的拉力大小为F,则此时( )| A. | 人拉绳行走的速度为vcosθ | B. | 人拉绳行走的速度为$\frac{v}{cosθ}$ | ||
| C. | 船的加速度为$\frac{Fcosθ-{F}_{t}}{m}$ | D. | 船的加速度为$\frac{Fsinθ-{F}_{t}}{m}$ |
| A. | α粒子散射实验证明了原子核是由质子和中子组成的 | |
| B. | 天然放射现象的发现揭示了原子的核式结构 | |
| C. | 普朗克在研究黑体辐射问题时提出了能量子假说 | |
| D. | 光电效应、康普顿效应说明光具有粒子性 |
| A. | 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上 | |
| B. | 对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积 | |
| C. | 所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等 | |
| D. | 以上说法都不对 |

 如图所示,A、B两辆汽车在笔直的公路上同向行驶,当B车在A车前s=84m处时,B车的速度vB=4m/s,且正以a=2m/s2的加速度做匀加速运动;经过一段时间后,B车的加速度突然变为零.A车一直以vA=20m/s的速度做匀速运动,从最初相距84m时开始计时,经过t0=12s后两车相遇.问B车加速行驶的时间是多少?
如图所示,A、B两辆汽车在笔直的公路上同向行驶,当B车在A车前s=84m处时,B车的速度vB=4m/s,且正以a=2m/s2的加速度做匀加速运动;经过一段时间后,B车的加速度突然变为零.A车一直以vA=20m/s的速度做匀速运动,从最初相距84m时开始计时,经过t0=12s后两车相遇.问B车加速行驶的时间是多少? 如图,光滑的水平面上有两个小球A、B,已知B的质量mB=3kg,A、B之间的距离x=2m.现给小球A一水平向右的初速度v0=2m/s,设A、B之间的碰撞时间极短,且为弹性碰撞.要使小球A从开始经t=3s时间又回到出发点,则小球A的质量mA为多少?
如图,光滑的水平面上有两个小球A、B,已知B的质量mB=3kg,A、B之间的距离x=2m.现给小球A一水平向右的初速度v0=2m/s,设A、B之间的碰撞时间极短,且为弹性碰撞.要使小球A从开始经t=3s时间又回到出发点,则小球A的质量mA为多少?