题目内容
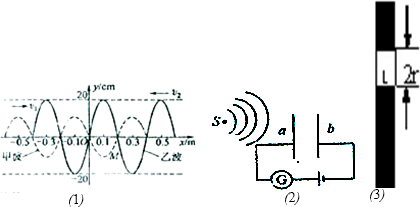
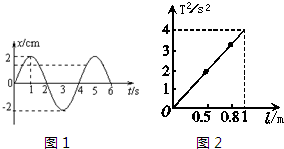 (1)一个质点做简谐运动的图象如图所示,质点振动频率为
(1)一个质点做简谐运动的图象如图所示,质点振动频率为0.25
0.25
Hz;在10s内质点经过的路程是20
20
cm; t=4.5s时刻质点的位移是| 2 |
| 2 |
零
零
(填零或最大),加速度最大
最大
(填零或最大)(2)在做“用单摆测定重力加速度”的实验中,某同学先测得摆线长为89.2cm,摆球的直径如图所示,然后用秒表记录了单摆做30次全振动.
①该单摆的摆长为
90.225
90.225
cm.②如果该同学测得的g值偏大,可能的原因是
ABD
ABD
A.测摆长时记录的是摆球的直径
B.开始计时时,秒表过迟按下
C.摆线上端牢固地系于悬点,摆动中出现松动,使摆线长度增加了
D.实验中误将29次全振动数为30次
③为了提高实验精度,在实验中可改变几次摆长l,测出相应的周期T,从而得出一组对应的l与T的数值,再以l为横坐标,T2为纵坐标,将所得数据连成直线如图所示,则测得的重力加速度g=
9.86
9.86
m/s2(结果保留三位有效数字)(3)另一同学在“用单摆测定重力加速度”的实验中,用的摆球密度不均匀,无法确定重心位置.他第一次量得悬线长为l1(不计半径),测得周期为T1;第二次量得悬线长为l2,测得周期为T2.根据上述数据,g=
| 4π2(l2-l1) | ||||
|
| 4π2(l2-l1) | ||||
|
分析:(1)由图象读出周期T,由f=
,求出频率.质点在一个周期内通过的路程是四个振幅,根据时间10s与周期的关系,求解路程.由数学知识求解t=4.5s时刻质点的位移.根据质点的位置分析速度和加速度.
(2)①单摆摆长等于摆线长度l与摆球的半径r之和,即L=l+r;②由单摆周期公式,求出重力加速度的表达式,根据重力加速度的表达式,分析重力加速度测量值偏大的原因.
(3)设摆球的重心到线与球结点的距离为r,根据单摆周期的公式分别列出方程,求解重力加速度.
| 1 |
| T |
(2)①单摆摆长等于摆线长度l与摆球的半径r之和,即L=l+r;②由单摆周期公式,求出重力加速度的表达式,根据重力加速度的表达式,分析重力加速度测量值偏大的原因.
(3)设摆球的重心到线与球结点的距离为r,根据单摆周期的公式分别列出方程,求解重力加速度.
解答:解:(1)由图知,T=4s,则频率f=
=0.25Hz.
n=
=
=2.5,而质点在一个周期内通过的路程是四个振幅,半个周期内通过的路程是两个振幅,故在10s内质点经过的路程是S=2.5×4A=20cm.
振动方程为y=Asin
t=2sin0.5πtcm,则t=4.5s时刻质点的位移是y=2sin0.5π×4.5cm=
cm.
在5s末,质点在正向最大位移处,则速度为零,加速度最大.
(2)①单摆摆长等于摆线长度l与摆球的半径r之和,即L=l+r=90.225cm;
②由单摆周期公式T=2π
,可知重力加速度g=
:
A、测摆长时记录的是摆球的直径,则摆长偏大,由g=
知,所测重力加速度偏大.故A正确.
B.开始计时时,秒表过迟按下,周期偏小,由g=
知,所测重力加速度偏大.故B正确.
C.摆线上端牢固地系于悬点,摆动中出现松动,使摆线长度增加了,T偏大,所测重力加速度偏小.故C错误.
D.实验中误将29次全振动数为30次,周期偏小,由g=
知,所测重力加速度偏大.故D正确.
故选ABD
(3)设摆球的重心到线与球结点的距离为r,根据单摆周期的公式T=2π
T1=2π
,T2=2π
联立两式解得 g=
故答案为:
(1)0.25,20,
,零,最大
(2)①90.225 ②ABD ③9.86 m/s2 (3)g=g=
| 1 |
| T |
n=
| t |
| T |
| 10 |
| 4 |
振动方程为y=Asin
| 2π |
| T |
| 2 |
在5s末,质点在正向最大位移处,则速度为零,加速度最大.
(2)①单摆摆长等于摆线长度l与摆球的半径r之和,即L=l+r=90.225cm;
②由单摆周期公式T=2π
|
| 4π2L |
| T2 |
A、测摆长时记录的是摆球的直径,则摆长偏大,由g=
| 4π2L |
| T2 |
B.开始计时时,秒表过迟按下,周期偏小,由g=
| 4π2L |
| T2 |
C.摆线上端牢固地系于悬点,摆动中出现松动,使摆线长度增加了,T偏大,所测重力加速度偏小.故C错误.
D.实验中误将29次全振动数为30次,周期偏小,由g=
| 4π2L |
| T2 |
故选ABD
(3)设摆球的重心到线与球结点的距离为r,根据单摆周期的公式T=2π
|
T1=2π
|
|
| 4π2(l2-l1) | ||||
|
故答案为:
(1)0.25,20,
| 2 |
(2)①90.225 ②ABD ③9.86 m/s2 (3)g=g=
| 4π2(l2-l1) | ||||
|
点评:第3题运用单摆周期公式分析处理实际问题,注意单摆的摆长等于摆球的重心到悬点的距离,不是摆线的长度.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
一个质点做简谐振动,它的振动图像如图4-1所示,下列判断正确的是( )
| A.图中的曲线部分是质点的运动轨迹 |
| B.有向线段OA是质点在t1时间内的位移 |
| C.振幅与有向线段OA在x轴的投影之差等于质点在t1时间内的位移大小 |
| D.有向线段OA的斜率是质点在t1时刻的瞬时速率 |
 中始终有方向不变的电流
中始终有方向不变的电流