Question

【题目】为了探究动能定理，一位同学设计了如图所示的实验装置．他先固定并调整斜槽，让末端O点的切线水平，再将一木板竖直放置并固定，木板到斜槽末端O的距离为s，使小球从斜槽上某一标记点由静止释放，若小球到达斜槽底端时下落的高度为H、小球从O点做平抛运动击中木板时下落的高度为y．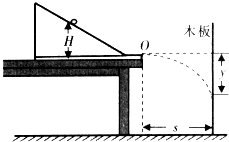

（1）假定斜槽光滑，小球由静止滑下到击中木板的过程中，满足动能定理的关系式为： ．
（2）若斜槽倾角为θ，小球与斜槽之间的动摩擦因数为μ（只考虑滑动摩擦力，且小球与水平槽之间的摩擦不计），小球由静止滑下到击中木板的过程中，满足动能定理的关系式是： ．
（3）改变小球在斜槽上的释放位置，进行多次测量，能得到多组关于H和y的数据，若以H为横坐标，从（1）、（2）中的关系式可知以为纵坐标，通过描点作图，能得到一条倾斜的直线．

Answer 1

【答案】
（1）H=
（2）（1﹣ ）H=
（3）
【解析】解：（1）当斜槽光滑时，只有小球的重力做功，由动能定理得：

mgH=

小球离开O点后做平抛运动，由平抛运动的规律有：

s=v1t1，y= ，

联立解得：H= ．（2）当斜槽粗糙时，重力对小球做正功，滑动摩擦力对小球做负功，由动能定理得：

mgH﹣μmgcosθ× =

由平抛运动知识有：s=v2t2，y= ，

联立解得：（1﹣ ）H= （3）根据上题的表达式可知如果以H为横坐标轴，则以 为纵坐标，将测量得到的多组数据通过描点作图，能得到一条倾斜的直线．

所以答案是：（1）H= ．（2）（1﹣ ）H= ．（3） ．