题目内容
 如图所示,带有轨道的凹槽放在水平面上,轨道ABDO处于竖直平面内,AB是半径为R的
如图所示,带有轨道的凹槽放在水平面上,轨道ABDO处于竖直平面内,AB是半径为R的| 1 | 4 |
(1)若凹槽固定在水平面内,且轨道光滑,求小球到达B点的速度
(2)若凹槽放在光滑水平面内,且轨道光滑,求小球通过B点时对轨道的压力
(3)若凹槽放在光滑水平面内,小球恰能通过O点,求小球通过轨道时克服阻力做的功?
分析:(1)小球运动到B点过程,只有重力做功,机械能守恒,根据机械能守恒定律列式求解即可;
(2)小球和凹槽系统水平方向动量守恒,根据动量守恒定律和系统机械能守恒定律列式求解出小球和凹槽的速度,根据向心力公式列式求解;
(3)小球和凹槽系统在水平方向不受外力,动量守恒;在最高点,重力提供向心力;再对整个过程运用功能关系列式求解.
(2)小球和凹槽系统水平方向动量守恒,根据动量守恒定律和系统机械能守恒定律列式求解出小球和凹槽的速度,根据向心力公式列式求解;
(3)小球和凹槽系统在水平方向不受外力,动量守恒;在最高点,重力提供向心力;再对整个过程运用功能关系列式求解.
解答:解:(1)由机械能守恒:mg(H+R)=
m
vB=
即小球到达B点的速度为
m
.
(2)由动量守恒定律:0=mv1-Mv2
由机械能守恒:mg(H+R)=
m
+
M
由圆周运动:若在B点左侧
N-mg=m
解得
N=mg+
由牛顿第三定律:N’=N=mg+
若在B点右侧
N-mg=N-mg=m
解得
N=mg+
由牛顿第三定律:N’=N=mg+
即小球通过B点左侧时对轨道的压力为mg+
,小球通过B点右侧时对轨道的压力mg+
.
(3)由动量守恒定律:0=mv1′-Mv2′
由圆周运动:mg=m
由能量守恒定律:mgH=
m
+
M
+Wf
解得
Wf=mgH-
mgR
故小球通过轨道时克服阻力做的功为mgH-
mgR
.
| 1 |
| 2 |
| v | 2 B |
vB=
| 2g(H+R) |
即小球到达B点的速度为
| 1 |
| 2 |
| v | 2 B |
(2)由动量守恒定律:0=mv1-Mv2
由机械能守恒:mg(H+R)=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
由圆周运动:若在B点左侧
N-mg=m
| (v1+v2)2 |
| R |
解得
N=mg+
| 2m(M+m)g(H+R) |
| MR |
由牛顿第三定律:N’=N=mg+
| 2m(M+m)g(H+R) |
| MR |
若在B点右侧
N-mg=N-mg=m
| (v1+v2)2 |
| 0.5R |
解得
N=mg+
| 4m(M+m)g(H+R) |
| MR |
由牛顿第三定律:N’=N=mg+
| 4m(M+m)g(H+R) |
| MR |
即小球通过B点左侧时对轨道的压力为mg+
| 2m(M+m)g(H+R) |
| MR |
| 4m(M+m)g(H+R) |
| MR |
(3)由动量守恒定律:0=mv1′-Mv2′
由圆周运动:mg=m
| (v1′+v2′)2 |
| 0.5R |
由能量守恒定律:mgH=
| 1 |
| 2 |
| v′ | 2 1 |
| 1 |
| 2 |
| v′ | 2 2 |
解得
Wf=mgH-
| 1 |
| 4 |
| M |
| M+m |
故小球通过轨道时克服阻力做的功为mgH-
| 1 |
| 4 |
| M |
| M+m |
点评:本题关键在于对凹槽与小球系统运用动量守恒定律和功能关系列方程,同时在最高点,合力提供向心力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
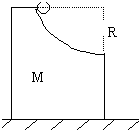 如图所示,带有光滑的半径为R的
如图所示,带有光滑的半径为R的
 图弧轨道的滑块静止在光滑的水平面上,此滑块质量为M,一只质量为m的小球由静止从A点释放,当小球从滑块B水平飞出时,滑块的反冲速度是多大?
图弧轨道的滑块静止在光滑的水平面上,此滑块质量为M,一只质量为m的小球由静止从A点释放,当小球从滑块B水平飞出时,滑块的反冲速度是多大?
 圆周轨道,半径OA处于水平位置,BDO是直径为R的半圆轨道.一个小球P从A点的正上方距水平半径OA高H处自由落下,由A点进入轨道.已知小球的质量为m,凹槽的质量为M,重力加速度为g.
圆周轨道,半径OA处于水平位置,BDO是直径为R的半圆轨道.一个小球P从A点的正上方距水平半径OA高H处自由落下,由A点进入轨道.已知小球的质量为m,凹槽的质量为M,重力加速度为g.