题目内容
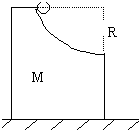 如图所示,带有光滑的半径为R的
如图所示,带有光滑的半径为R的| 1 | 4 |
分析:滑块与圆弧轨道水平方向不受外力,系统动量守恒;系统中只有重力势能向动能转化,机械能守恒;根据守恒定律列方程后联立求解.
解答:解:m运动过程中,其机械能是不守恒的,因为m的重力势能转化为m和M的动能,故应是m和M组成的系统机械能守恒,又因为水平方向系统合外力为零,故系统水平方向动量守恒,取圆弧轨道最低点为零势能点,有:
mgR=
m
+
M
又由动量守恒定律得:
mv1-Mv2=0
联立解得:v2=
.(负值舍去)
答:当小球从滑块B水平飞出时,滑块的反冲速度是
.
mgR=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
又由动量守恒定律得:
mv1-Mv2=0
联立解得:v2=
| m |
| M |
|
答:当小球从滑块B水平飞出时,滑块的反冲速度是
| m |
| M |
|
点评:本题关键是明确滑块和轨道系统动量守恒、机械能也守恒,然后根据守恒定律列方程联立求解.

练习册系列答案
相关题目
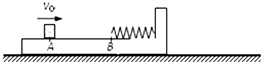 如图所示,带有挡板的长木板置于光滑水平面上,轻弹簧放置在木板上,右端与挡板相连,左端位于木板上的B点.开始时木板静止,小铁块从木板上的A点以速度v0=4.0m/s正对着弹簧运动,压缩弹簧,弹簧的最大形变量xm=0.10m;之后小铁块被弹回,弹簧恢复原长;最终小铁块与木板以共同速度运动.已知当弹簧的形变量为x时,弹簧的弹性势能
如图所示,带有挡板的长木板置于光滑水平面上,轻弹簧放置在木板上,右端与挡板相连,左端位于木板上的B点.开始时木板静止,小铁块从木板上的A点以速度v0=4.0m/s正对着弹簧运动,压缩弹簧,弹簧的最大形变量xm=0.10m;之后小铁块被弹回,弹簧恢复原长;最终小铁块与木板以共同速度运动.已知当弹簧的形变量为x时,弹簧的弹性势能 如图所示,在光滑的水平面上放置A、B两个物体,其中B物体带有一个质量不计的弹簧.A的物体质量为m,当物体A以速度v向着B运动,并压缩弹簧,在压缩弹簧的过程中,下面说法正确的是( )
如图所示,在光滑的水平面上放置A、B两个物体,其中B物体带有一个质量不计的弹簧.A的物体质量为m,当物体A以速度v向着B运动,并压缩弹簧,在压缩弹簧的过程中,下面说法正确的是( )
 图弧轨道的滑块静止在光滑的水平面上,此滑块质量为M,一只质量为m的小球由静止从A点释放,当小球从滑块B水平飞出时,滑块的反冲速度是多大?
图弧轨道的滑块静止在光滑的水平面上,此滑块质量为M,一只质量为m的小球由静止从A点释放,当小球从滑块B水平飞出时,滑块的反冲速度是多大?