题目内容
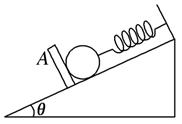
(8分)如图所示,在倾角为θ的光滑斜面上端系有一劲度系数为k的轻质弹簧,弹簧下端连一个质量为m的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以加速度a(a<gsinθ)沿斜面向下匀加速运动,问:
(1)小球向下运动多少距离时速度最大?
(2)从开始运动到小球与挡板分离所经历的时间为多少?

(1)小球向下运动多少距离时速度最大?
(2)从开始运动到小球与挡板分离所经历的时间为多少?
(1)xm=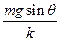
(2)t=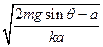
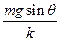
(2)t=
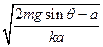
(1)球和挡板分离后做加速度减小的加速运动,当加速度为零时,速度最大,此时物体所受合力为零.
即kxm=mgsinθ, (2分)
解得xm=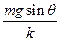 . (1分)
. (1分)
(2)设球与挡板分离时位移为s,经历的时间为t,从开始运动到分离的过程中,m受竖直向下的重力,垂直斜面向上的支持力FN,沿斜面向上的挡板支持力F1和弹簧弹力F.
据牛顿第二定律有mgsinθ-F-F1=ma, (1分)
F=kx. (1分)
随着x的增大,F增大,F1减小,保持a不变,当m与挡板分离时,x增大到等于s,F1减小到零,则有: mgsinθ-ks=ma, (1分)
又: s=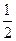 at2 (1分)
at2 (1分)
联立解得:mgsinθ-k·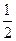 at2=ma,
at2=ma,
t=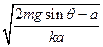 . (1分)
. (1分)
即kxm=mgsinθ, (2分)
解得xm=
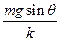 . (1分)
. (1分)(2)设球与挡板分离时位移为s,经历的时间为t,从开始运动到分离的过程中,m受竖直向下的重力,垂直斜面向上的支持力FN,沿斜面向上的挡板支持力F1和弹簧弹力F.
据牛顿第二定律有mgsinθ-F-F1=ma, (1分)
F=kx. (1分)
随着x的增大,F增大,F1减小,保持a不变,当m与挡板分离时,x增大到等于s,F1减小到零,则有: mgsinθ-ks=ma, (1分)
又: s=
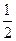 at2 (1分)
at2 (1分)联立解得:mgsinθ-k·
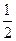 at2=ma,
at2=ma,t=
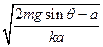 . (1分)
. (1分)
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目

 ,绳BC长度为b。两绳能够承受的最大拉力均为2mg。求:
,绳BC长度为b。两绳能够承受的最大拉力均为2mg。求:


 物块A刚滑上长木板B到二者刚好相对静止时小物块的位移的大小。
物块A刚滑上长木板B到二者刚好相对静止时小物块的位移的大小。
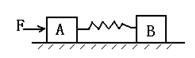

 。中间用细绳l、2连接,现用一水平恒力F作用在C上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,则下列说法正确的是
。中间用细绳l、2连接,现用一水平恒力F作用在C上,三者开始一起做匀加速运动,运动过程中把一块橡皮泥粘在某一木块上面,系统仍加速运动,则下列说法正确的是