��Ŀ����
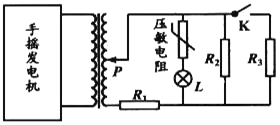
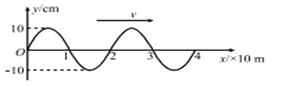
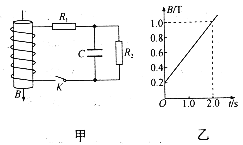
����Ŀ������ͼ����ʾ�ĵ�·�У����߹�����n=1000�ѣ�������S=20cm2�����߹ܵ��ߵ���r=1.0����R1=4.0����R2=5.0����C=30��F����һ��ʱ���ڣ���ֱ�������߹ܵĴų��ĴŸ�Ӧǿ��B�ķ�����ͼ����ʾ����С����ͼ����ʾ�Ĺ��ɱ仯������˵������ȷ����
A. ���߹��в����ĸ�Ӧ�綯��Ϊ1.2V
B. �պ�K����·�еĵ����ȶ���������¼��������
C. �պ�K����·�еĵ����ȶ�����R1�ĵ繦��Ϊ2.56��10��2W
D. K�Ͽ�������R2�ĵ���Ϊ1.8��10-2C
���𰸡�C
��������
A�����ݷ����ڵ�Ÿ�Ӧ���ɣ�![]() ����ã�E=0.8V����A����
����ã�E=0.8V����A����
B��������ζ��ɿ�֪�����߹ܵĸ�Ӧ�����������£������߹��¶��ǵ�Դ����������ô�������¼������磬��B����
C������ȫ��·ŷķ���ɣ��У�I=![]() =0.08A������P=I2R1��ã�P=2.56��10-2W����C��ȷ��
=0.08A������P=I2R1��ã�P=2.56��10-2W����C��ȷ��
D��S�Ͽ�������R2�ĵ�����ΪS�պ�ʱC���������ĵ���Q�����������˵ĵ�ѹΪ��U=IR2=0.4V������R2�ĵ���Ϊ��Q=CU=1.2��10-5C����D����

��ϰ��ϵ�д�
 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�
�����Ŀ