题目内容
【题目】(1)试证明:“静止的通电导线在磁场中受到的安培力,在数值上等于大量定向运动的电荷受到的洛伦兹力的总和”。以一段柱状通电直导线为例,设导线的横截面积为S,长度为L,单位体积内自由电荷数为n,电荷电量为q,电荷定向移动的平均速率为v。假定在金属导体中正电荷定向移动形成电流,得到结果具有普遍性(本假定同样适用于以下两问)。
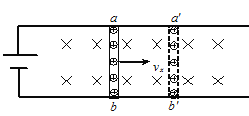
(2)如图所示,接通电路后,导体棒在安培力作用下向右运动。此时,导体中自由电荷既在电场力作用下沿导体棒运动,又随导体棒沿水平方向运动,从而导致运动电荷所受洛伦兹力与宏观安培力不在同一方向。
在此模型中,请证明:安培力对导体棒做功,在数值上等于大量可自由运动电荷所受洛伦兹力的某个分力对电荷做功的总和。
为方便证明,可设电源电动势为E,导体棒的电阻为R,其长度为L,恰好等于平行轨道间距,整个装置处于竖直、向下磁感应强度为B的匀强磁场中,忽略电源和金属导轨的电阻。导体棒在安培力和摩擦力的作用下,向右以速度vx做匀速直线运动,在时间t内由实线位置运动到虚线位置;同时棒内某个正电荷在该时间t内从a位置定向运动到b位置。如在证明过程中,还需用到其他物理量,请自行假设。
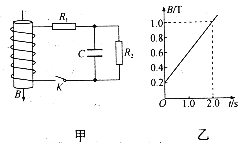
(3)在(2)问所涉及的模型中,通过导体棒的电流:![]() 。这是因为导体在运动过程中会切割磁感线,产生“反电动势E”。请你根据该过程的微观机制,利用电动势的定义,求出图示模型中的反电动势E,并写出通过导体棒的电流I。
。这是因为导体在运动过程中会切割磁感线,产生“反电动势E”。请你根据该过程的微观机制,利用电动势的定义,求出图示模型中的反电动势E,并写出通过导体棒的电流I。
【答案】(1)证明过程见解析;(2)证明过程见解析;(3)![]() ;
;![]() 。
。
【解析】
(1)写出安培力和洛仑兹力的公式,将电流的微观表达式代入安培力公式可证明是洛仑兹力的整数倍;
(2)根据图示模型画出正电荷的速度矢量图,再由左手定则画出洛仑兹力矢量分解图,由功的定义,可以证明:安培力对导体棒做功,在数值上等于大量可自由运动电荷所受洛伦兹力的水平分力对电荷做功的总和;
(3)由电动势的定义,及欧姆定律先求出反电动势,然后再写出电路中的电流。
:(1)证明:通电导线在磁场中受到的安培力为:![]()
而电流为:![]()
每个电荷q受到的洛仑兹力为:![]()
所以安培力为:![]()
(2)如图所示的模型中,导体棒通电后受到安培力向右运动距离为![]() ,则安培力做功为:
,则安培力做功为:
![]()
正电荷的和速度如图所示(下),及洛伦兹力如图所示(上),则洛伦兹力水平分量为:
![]()
它所做的功为:![]()
所以:![]()
即安培力做功在数值上等于大量运动电荷所受洛伦兹力在导体棒运动方向上分力做功之和。
(3)根据电动势的定义有:![]()
电路中电流为:![]()

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
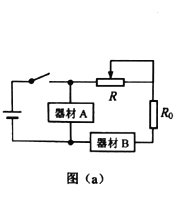
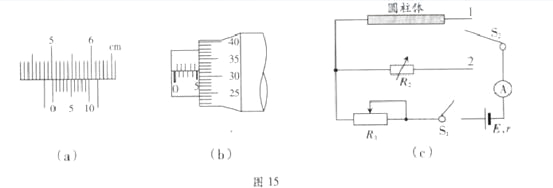
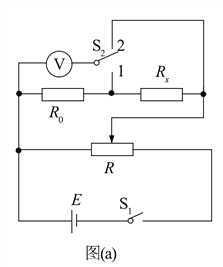
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】一课外实验小组用如图所示的电路测量某待测电阻Rx的阻值,图中R0为标准定值电阻(R0=20.0 Ω);![]() 可视为理想电压表。S1为单刀开关,S2位单刀双掷开关,E为电源,R为滑动变阻器。采用如下步骤完成实验:
可视为理想电压表。S1为单刀开关,S2位单刀双掷开关,E为电源,R为滑动变阻器。采用如下步骤完成实验:
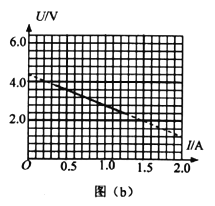
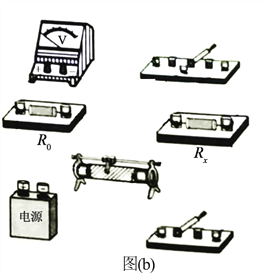
(1)按照实验原理线路图(a),将图(b)中实物连线_____________;
(2)将滑动变阻器滑动端置于适当位置,闭合S1;
(3)将开关S2掷于1端,改变滑动变阻器动端的位置,记下此时电压表![]() 的示数U1;然后将S2掷于2端,记下此时电压表
的示数U1;然后将S2掷于2端,记下此时电压表![]() 的示数U2;
的示数U2;
(4)待测电阻阻值的表达式Rx=_____________(用R0、U1、U2表示);
(5)重复步骤(3),得到如下数据:
1 | 2 | 3 | 4 | 5 | |
U1/V | 0.25 | 0.30 | 0.36 | 0.40 | 0.44 |
U2/V | 0.86 | 1.03 | 1.22 | 1.36 | 1.49 |
| 3.44 | 3.43 | 3.39 | 3.40 | 3.39 |
(6)利用上述5次测量所得![]() 的平均值,求得Rx=__________Ω。(保留1位小数)
的平均值,求得Rx=__________Ω。(保留1位小数)