题目内容
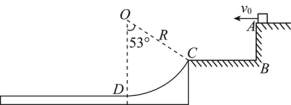
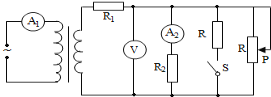
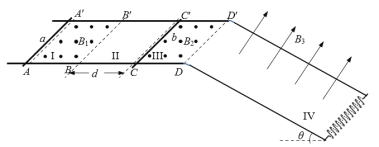
【题目】如图所示,在水平面内有两根间距为l的金属导轨平行放置,导轨末端通过一小段塑料接口与足够长的倾斜平行金属导轨平滑连接,倾角为θ。在区域Ⅰ,Ⅲ和Ⅳ中,存在垂直于导轨向上的匀强磁场,磁感应强度分别为B1,B2和B3;区域Ⅱ中导轨粗糙,宽度为d。其余部分均光滑。磁场边界AA′上放置金属棒a,磁场边界CC′右侧附近静止放置金属棒b,倾斜导轨足够远处连接有电感为L的电感线圈。现让金属棒a以初速度v0进入磁场,发现它最终刚好停在了CC′(边界左侧),而金属棒b恰能滑入倾斜轨道。已知金属棒a与轨道粗糙部分的动摩擦因数为,金属棒a的电阻为R,其余电阻均不计,金属棒a、b的质量均为m,重力加速度取g,求:
(1)在金属棒a刚进入磁场瞬间,金属棒b的加速度;
(2)金属棒a在离开区域Ⅰ后产生的焦耳热Q;
(3)金属棒b能沿倾斜导轨向下滑行的最大距离xm。(已知自感线圈的自感电动势![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)a棒进入磁场瞬间,产生电动势和电流分别为
![]() ,
,![]()
所以棒b受到的安培力为
![]()
由牛顿第二定律得
![]()
解得
![]()
(2)设金属棒a离开磁场Ⅰ区域时的速度为v1,此时金属棒b的速度为v2,金属棒a在区域Ⅱ中做匀减速运动,可得
![]()
棒a穿越磁场区域Ⅰ过程中,由动量定理可得
![]()
根据题意有
![]()
联立解得
![]()
对棒b,在该过程中,由动量定理可得
![]()
解得
![]()
之后,由能量关系可知,克服安培力做的功等于电路中产生的焦耳热,金属棒b此时的动能将全部转化成金属棒a的焦耳热Q,有
![]()
解得
![]()
(3)金属棒b恰能滑入斜轨,则在斜轨上初速度为0,开始下滑,因为b棒与线圈组成的回路,直流电阻为零,所以必须满足
![]()
可得
![]()
所以棒开始运动后棒上电流与棒的位移成正比,即
![]()
所以棒的运动方程为
![]()
可知金属棒做简谐运动,平衡位置时,a=0,即
![]()
由简谐运动对称性可知,下滑最大距离为
![]()