题目内容
如图所示,一根长为4m的均匀直棒AO,O端用光滑铰链固定于地面上,上端有一水平拉力F,为了使棒能垂直地立在地面上,用一根长为4m的绳子拉住棒,若绳与水平方向的夹角为30°,则绳子的拉力大小为 F,要使绳子拉力最小,则绳的另一端系在杆上的位置距地面的高度为 m.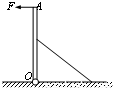
【答案】分析:以O点转轴,根据力矩平衡的条件列式求出绳子的拉力;
解答:解:以O点转轴,根据力矩平衡的条件得
F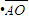 =T?Lsin30°cos30°
=T?Lsin30°cos30°
则得:绳子拉力T=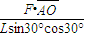 =
=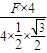 =
=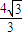 F
F
设绳子与水平方向的夹角为α时,则有F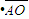 =T?Lsinαcosα.
=T?Lsinαcosα.
则得 T=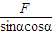 =
=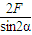
当α=45°时,绳子拉力T最大,此时绳的另一端系在杆上的位置距地面的高度h=Lsinα=2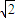 m.
m.
故答案为: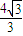 F,2
F,2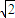 .
.
点评:本题是力矩平衡问题,关键要正确确定力臂的大小,运用函数法求绳子拉力的最小值.
解答:解:以O点转轴,根据力矩平衡的条件得
F
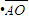 =T?Lsin30°cos30°
=T?Lsin30°cos30°则得:绳子拉力T=
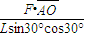 =
=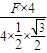 =
=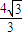 F
F设绳子与水平方向的夹角为α时,则有F
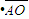 =T?Lsinαcosα.
=T?Lsinαcosα.则得 T=
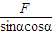 =
=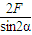
当α=45°时,绳子拉力T最大,此时绳的另一端系在杆上的位置距地面的高度h=Lsinα=2
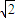 m.
m.故答案为:
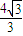 F,2
F,2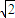 .
.点评:本题是力矩平衡问题,关键要正确确定力臂的大小,运用函数法求绳子拉力的最小值.

练习册系列答案
相关题目
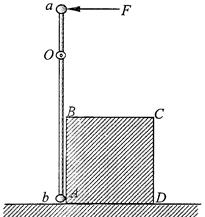
 (2012?杨浦区一模)如图所示,一根长为三的细刚性轻杆的两端分别连结小球a和b,它们的质量分别为ma和mb,杆可绕距a球为L/4处的水平定轴D在竖直平面内转动,初始时杆处于竖直位置,小球b几乎接触桌面,在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面.现用一水平恒力F作用于a球上,使之绕O轴逆时针转动,设在此过程中立方体物块没有发生转动,且小球b立方体物块始终接触没有分离.不计一切摩擦,求:
(2012?杨浦区一模)如图所示,一根长为三的细刚性轻杆的两端分别连结小球a和b,它们的质量分别为ma和mb,杆可绕距a球为L/4处的水平定轴D在竖直平面内转动,初始时杆处于竖直位置,小球b几乎接触桌面,在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面.现用一水平恒力F作用于a球上,使之绕O轴逆时针转动,设在此过程中立方体物块没有发生转动,且小球b立方体物块始终接触没有分离.不计一切摩擦,求: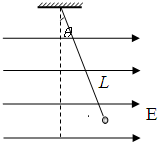 如图所示,一根长为L的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场当中,电场强度大小为E,方向是水平向右,已知:当细线偏离竖直方向为θ角时,小球处于平衡状态,试求:
如图所示,一根长为L的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场当中,电场强度大小为E,方向是水平向右,已知:当细线偏离竖直方向为θ角时,小球处于平衡状态,试求: