题目内容
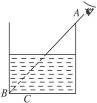
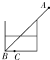
如图所示,一储油圆桶,底面直径与桶高均为d,当桶内无油时,从某点A恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距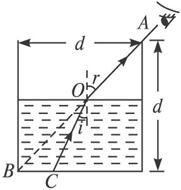
解析:只要某点发出的光或反射的光能进入观察者的眼睛,眼睛便能观察到该点.桶内没装液体时,B点发出的光是沿直线到达A点的,C点发出的光也是沿直线传播的,无法通过A点,在A点的眼睛就看不到它.装上半桶油后,C点发出的光将会折射到A点,如上图所示,由光路图可知:

sini=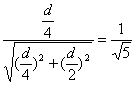
sinr=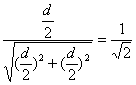
根据折射定律得:n=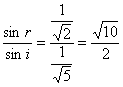
光在油中的传播速度:v=![]() ×107m/s.
×107m/s.
答案:![]() 6
6![]() ×107
×107

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 (2008?湛江二模)如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高的一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距
(2008?湛江二模)如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高的一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距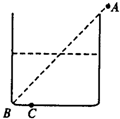 如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点A恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距d/4.由此可得油的折射率n=
如图所示,一储油圆桶,底面直径与桶高均为d.当桶内无油时,从某点A恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高一半时,在A点沿AB方向看去,看到桶底上的C点,C、B相距d/4.由此可得油的折射率n=