题目内容
如图15所示,发射人造卫星时,先把卫星送入近地点Q,然后使其沿椭圆轨道到达远地点P,此时速度为v.若P点到地心的距离为R,卫星的总质量为m,地球半径为R0,地表的重力加速度为g,则欲使卫星从P点起绕地球做半径为R的圆轨道运动,卫星在P点处应将质量为Δm的燃气以多大的对地速度向后喷出?(将连续喷气等效为一次性喷气)
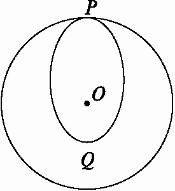
图15

图15
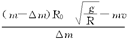
以卫星和喷出的燃气Δm为系统,系统在运动方向上不受外力作用,在该方向上动量守恒.取卫星在P点的运动方向为正方向,设喷气速度大小为v1,卫星因反冲而达到的速度为v2,由动量守恒定律有:mv=(m-Δm)v2+Δm(-v1),做圆周轨道运动的条件是: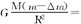
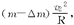 由牛顿第二定律和万有引力定律有:
由牛顿第二定律和万有引力定律有: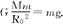 解以上各式得:v1
解以上各式得:v1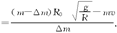
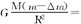
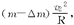 由牛顿第二定律和万有引力定律有:
由牛顿第二定律和万有引力定律有: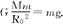 解以上各式得:v1
解以上各式得:v1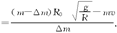

练习册系列答案
相关题目
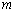 的物体以初速度
的物体以初速度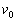 开始做平抛运动,经过时间
开始做平抛运动,经过时间 ,下降的高度为
,下降的高度为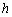 ,速度变为
,速度变为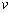 ,则这段时间内物体动量变化大小为( )
,则这段时间内物体动量变化大小为( )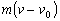
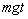
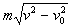
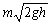
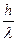 ,设太阳光垂直射到太阳帆板上,飞船总质量为m,求飞船的加速度.
,设太阳光垂直射到太阳帆板上,飞船总质量为m,求飞船的加速度.
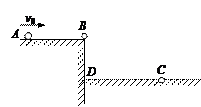
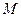
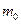
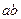
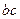
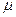
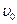
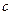
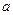
 表示),
表示),