题目内容
【题目】如图所示,直杆长L1=0.5m,圆筒高为L2=2.75m.直杆位于圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.试求:(取g=10m/s2 , )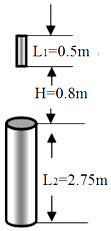
(1)直杆下端刚好开始进入圆筒时的瞬时速度v1 .
(2)直杆穿越圆筒所用的时间t.
【答案】
(1)解:杆做自由落体运动,由运动学知识得:v12=2gH
解得:v1= ![]() =4m/s
=4m/s
答:直杆下端刚好开始进入圆筒时的瞬时速度v1
(2)解:直杆下端到达圆筒上方到直杆上端离开圆筒下方所下落的距离为:
h=L1+L2=0.5m+2.75m=3.25m
设直杆穿越圆筒所用的时间为t,则有:
h=v1t+ ![]() gt2
gt2
代入数据为:3.25=4t+ ![]()
解得:t=0.5s
答:直杆穿越圆筒所用的时间t为0.5s
【解析】(1)直杆下落时做自由落体运动,根据位移﹣速度即可求得速度v1;(2)直杆穿越圆筒所用的时间应为下落的总时间减去直杆下端到达圆筒上方的时间,可根据位移﹣时间公式求解.
【考点精析】通过灵活运用自由落体运动和匀变速直线运动的速度、位移、时间的关系,掌握(1)条件:初速度为零,只受重力作用;(2)性质:是一种初速为零的匀加速直线运动,a=g;速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值即可以解答此题.

练习册系列答案
相关题目