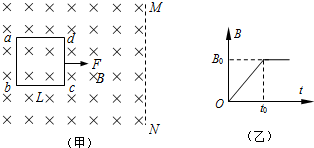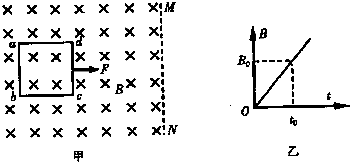题目内容
如图所示,MN为一水平面,O点左侧是粗糙的,O点右侧是光滑的,一轻质弹簧右端固定在墙壁上,左端与质量为m的小物体A相连,A静止在O点时,弹簧处于原长状态.另一质量也为m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动.已知物块A、B与水平面的粗糙部分MO间的滑动摩擦力大小均为F/4,物块运动到D时撤去外力F.已知CO=4s,OD=s,试求撤去外力后(A、B碰后速度相同但不黏连)(1)弹簧的最大弹性势能;
(2)物块B最终离O点的距离.

(1)Ep=![]() Fs (2)5s
Fs (2)5s
(1)设B和A相碰前的速度为v0,对B由动能定理得
(F-![]() F)×4s=
F)×4s=![]() mv02
mv02
得v0=![]()
B和A相碰时,由动量守恒得
mv0=2mv1(1分)
得v1=![]()
![]()
从碰后到A、B减速为0时弹簧具有最大弹性势能,由能量守恒得
Fs+![]() ×2mv12=Ep
×2mv12=Ep
得Ep=![]() Fs.
Fs.
(2)设撤去外力F后,A、B一起回到O点时的速度为v2,由机械能守恒得
Ep=![]() ×2mv22
×2mv22
v2=![]()
在返回O点时,A、B开始分离,B在滑动摩擦力作用下向左做匀减速运动,设物块B距O点为L时停止运动.
由动能定理得-![]() FL=0-
FL=0-![]() mv22
mv22
L=5s.

练习册系列答案
相关题目
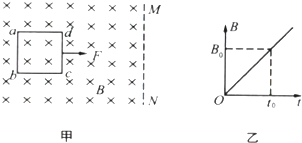 (2013?厦门一模)如图甲所示,一正方形单匝线框abcd放在光滑绝缘水平面上,线框边长为L、质量为m、电阻为R,该处空间存在一方向垂直纸面向里的匀强磁场,其右边界MN平行于ab,磁感应强度B随时间t变化的规律如图乙所示,已知
(2013?厦门一模)如图甲所示,一正方形单匝线框abcd放在光滑绝缘水平面上,线框边长为L、质量为m、电阻为R,该处空间存在一方向垂直纸面向里的匀强磁场,其右边界MN平行于ab,磁感应强度B随时间t变化的规律如图乙所示,已知 (2013?滨州一模)如图所示,一正方形单匝线框abcd放在光滑绝缘水平面上,线框边长为L、质量为m、电阻力R.该处空间存在一方向竖直向下的匀强磁场,其右边界MN平行于ab,磁感应强度大小为B.在一水平拉力作用下,线框从图示位置由静止开始向右做匀加速直线运动,直至全部离开磁场,线框的加速度大小为a,经过时间t线框cd边刚好离开边界MN,求:
(2013?滨州一模)如图所示,一正方形单匝线框abcd放在光滑绝缘水平面上,线框边长为L、质量为m、电阻力R.该处空间存在一方向竖直向下的匀强磁场,其右边界MN平行于ab,磁感应强度大小为B.在一水平拉力作用下,线框从图示位置由静止开始向右做匀加速直线运动,直至全部离开磁场,线框的加速度大小为a,经过时间t线框cd边刚好离开边界MN,求: