题目内容
如图甲所示，空间存在B=0.5T，方向竖直向下的匀强磁场，MN、PQ是处于同一水平面内相互平行的粗糙长直导轨，间距L=0.2m，R是连接在导轨一端的电阻，ab是跨接在导轨上质量为m=0.1kg的导体棒．从零时刻开始，通过一小型电动机对ab棒施加一个牵引力F，方向水平向左，使其从静止开始沿导轨做加速运动，此过程中棒始终保持与导轨垂直且接触良好．图乙是棒的v-t图象，其中OA段是直线，AC是曲线，小型电动机在12s末达到额定功率P=4.5W，此后保持功率不变．除R外，其余部分电阻均不计，g=10m/s2.
(1)求导体棒ab在0～12s内的加速度大小；
(2)求导体棒ab与导轨间的动摩擦因数及电阻R的值；
(3)请在答卷上作出牵引力的功率随时间（P—t）的变化图线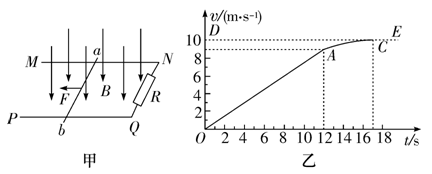
0.75m/s2 动摩擦因数为0.2 电阻阻值0.4欧
图像是0—12S过原点的抛物线（但抛物线的顶点不是原点）12S后功率恒定。
解析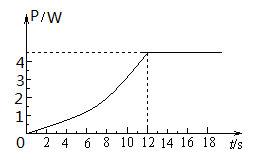
（1）由图象知12s末导体棒ab的速度为v1=9m/s，在0－12s内的加速度大小为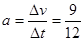
m/s2=0.75m/s2 ①
（2）t1=12s时，导体棒中感应电动势为
E=BLv1 ② （1分） 感应电流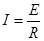
③
导体棒受到的安培力F1=BIL 即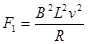
④
此时电动机牵引力为
⑤
由牛顿第二定律得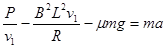
⑥
由图象知17s末导体棒ab的最大速度为v2=10m/s，此时加速度为零，同理有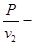
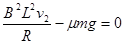⑦
由①②两式解得μ=0.2，R=0.4Ω⑧
（3）0－12s内，导体棒做匀加速运动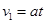
⑧
由⑥⑧⑧可得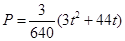
，可知0－12s内，牵引力的功率随时间的变化图线为过原点的抛物线，12S后功率恒定为4.5W 。如图：
练习册系列答案
相关题目
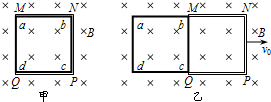（2006?泰州模拟）如图甲所示，空间存在着一个范围足够大的竖直向下的匀强磁场，磁场的磁感强度大小为B．边长为l的正方形金属框abcd（下简称方框）放在光滑的水平地面上，其外侧套着一个与方框边长相同的U形金属框架MNPQ（下简称U形框），U形框与方框之间接触良好且无摩擦．两个金属框每条边的质量均为m，每条边的电阻均为r．
如图甲所示，空间存在着以x=0平面为理想分界面的两个匀强磁场，左右两边磁场的磁感应强度分别为B1和B2，且B1：B2=4：3．方向如图，现在原点O处有一静止的中性粒子，突然分裂成两个带电粒子a和b，已知a带正电荷，分裂时初速度方向沿x轴正方向．若a粒子在第4次经过y轴时，恰与b粒子相遇．（1）在图乙中，画出a粒子的运动轨迹及用字母c标出a、b两粒子相遇的位置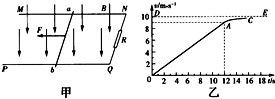
如图甲所示，空间存在B=0.5T、方向竖直向下的匀强磁场，MN、PQ是相互平行的粗糙的长直导轨，它们处于同一水平面内，其间距L=0.2m，R是连在导轨一端的电阻，ab是跨接在导轨上质量m=0.1kg的导体棒，从零时刻开始，通过一小型电动机对ab棒施加一个牵引力F，方向水平向左，使其从静止开始沿导轨做直线运动，此过程中棒始终保持与导轨垂直且接触良好，图乙是棒的速度一时间图象，其中OA段是直线，AC段是曲线，DE是曲线图象的渐近线，小型电动机在12s末达到额定功率P=4.5W，此后功率保持不变．导体棒和导轨的电阻均不计，g取10m/s2．