题目内容
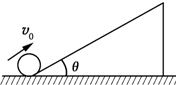 如图所示,小球以某一初速度v0沿固定光滑斜面从底端向上运动,已知斜面倾角为θ=30°,小球经过时间t返回到原出点,那么,小球到达最大高度一半处的速度大小为( )
如图所示,小球以某一初速度v0沿固定光滑斜面从底端向上运动,已知斜面倾角为θ=30°,小球经过时间t返回到原出点,那么,小球到达最大高度一半处的速度大小为( )分析:小球在光滑的斜面先上滑和后下滑,两个过程的加速度相同,具有对称性,上滑和下滑过程所用时间相等,由牛顿第二定律求出加速度大小,由运动学公式求出斜面的长度,再求解小球到达最大高度一半处的速度大小.
解答:解:由题得知,小球运动具有对称性,则小球下滑的时间为
.由牛顿第二定律得,小球在斜面上运动的加速度大小为:a=
=0.5g
则斜面的长度为:L=
a(
)2=
当小球到达最大高度一半时,离斜面顶端的距离为
,设此时速度大小为v,则有:
v2=2a?
得:v=
=
=
gt
选项ABD错误,C正确.
故选C
| t |
| 2 |
| mgsinθ |
| m |
则斜面的长度为:L=
| 1 |
| 2 |
| t |
| 2 |
| gt2 |
| 16 |
当小球到达最大高度一半时,离斜面顶端的距离为
| L |
| 2 |
v2=2a?
| L |
| 2 |
得:v=
| aL |
|
| ||
| 8 |
选项ABD错误,C正确.
故选C
点评:本题运用牛顿第二定律和运动学公式解决动力学问题,关键要抓住小球运动的对称性,得到小球下滑的时间.也可以通过作速度图象,结合运动学公式求解.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
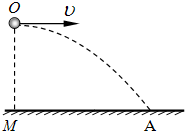 如图所示,小球以某一初速度v从水平地面上方O点水平抛出,M是O在地面上的竖直投影.小球落在地面上A点时的速度为v′,方向与水平面夹角为θ.若不计空气阻力,则( )
如图所示,小球以某一初速度v从水平地面上方O点水平抛出,M是O在地面上的竖直投影.小球落在地面上A点时的速度为v′,方向与水平面夹角为θ.若不计空气阻力,则( )
 如图所示,小球以某一初速度v沿固定光滑斜面从底端向上运动,已知斜面倾角为θ=30°,小球经过时间t返回到原出点,那么,小球到达最大高度一半处的速度大小为( )
如图所示,小球以某一初速度v沿固定光滑斜面从底端向上运动,已知斜面倾角为θ=30°,小球经过时间t返回到原出点,那么,小球到达最大高度一半处的速度大小为( )



