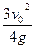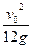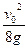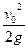题目内容
如图甲所示,一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ=370,t=0时刻有一物块沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示。若物块恰能到达M点,(取g=10m/s2,sin370=0.6,cos370=0.8),求:
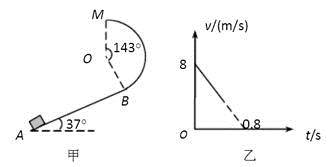
(1)物块经过B点时的速度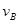 ;
;
(2)物块与斜面间的动摩擦因数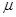 ;
;
(3)AB间的距离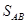 。
。

(1)物块经过B点时的速度
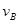 ;
;(2)物块与斜面间的动摩擦因数
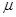 ;
;(3)AB间的距离
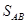 。
。(1)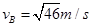
(2)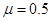
(3)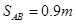
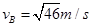
(2)
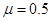
(3)
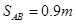
(1)由题意知:
在M点有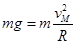 (1’)
(1’)
由机械能守恒定律:
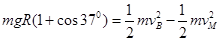 (1’)
(1’)
代入数据可求得: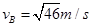 (1’)
(1’)
(2)v-t图可知物块运动的加速度 a=10m/s2 (1’)
由牛顿第二定律:
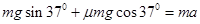 (1’)
(1’)
∴ 物块与斜面间的动摩擦因数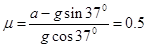 (1’)
(1’)
(3)由运动学公式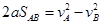 (1’)
(1’)
又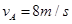
∴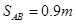 (1’)
(1’)
在M点有
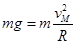 (1’)
(1’)由机械能守恒定律:
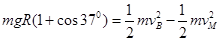 (1’)
(1’)代入数据可求得:
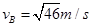 (1’)
(1’)(2)v-t图可知物块运动的加速度 a=10m/s2 (1’)
由牛顿第二定律:
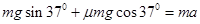 (1’)
(1’) ∴ 物块与斜面间的动摩擦因数
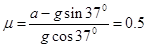 (1’)
(1’)(3)由运动学公式
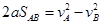 (1’)
(1’)又
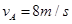
∴
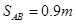 (1’)
(1’)
练习册系列答案
相关题目
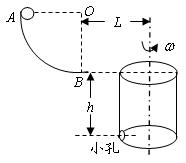
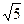 m/s,试求它通过B点速率的最小值。
m/s,试求它通过B点速率的最小值。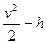 图线是__________,该线的斜率是__________.
图线是__________,该线的斜率是__________.