题目内容
4.两颗行星A和B各有一颗卫星a和b,卫星轨道接近各自行星的表面,如果两行星的质量之比为$\frac{{M}_{A}}{{M}_{B}}$=P,两行星半径之比为$\frac{{R}_{A}}{{R}_{B}}$=q,则两个卫星的周期之比$\frac{{T}_{a}}{{T}_{b}}$为( )| A. | $\sqrt{Pq}$ | B. | q$\sqrt{\frac{1}{P}}$ | C. | p$\sqrt{\frac{P}{q}}$ | D. | q$\sqrt{\frac{q}{P}}$ |
分析 由万有引力提供向心力,得周期与半径之间的关系可确定周期之比.
解答 解:由$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$ 可得:T=$2π\sqrt{\frac{{r}^{3}}{GM}}$
得两个卫星的周期之比为:$\frac{{T}_{a}}{{T}_{b}}$=$\sqrt{\frac{{r}_{a}^{3}}{{r}_{b}^{3}}\frac{{M}_{b}}{{M}_{a}}}$=$q\sqrt{\frac{q}{p}}$
故选:D
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行之比.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
14. 如图,放在只有右边有边界的匀强磁场内的矩形线圈,其转轴OO′恰好在磁场的边界上.若要线圈中产生感应电流,下列方法中可行的是( )
如图,放在只有右边有边界的匀强磁场内的矩形线圈,其转轴OO′恰好在磁场的边界上.若要线圈中产生感应电流,下列方法中可行的是( )
 如图,放在只有右边有边界的匀强磁场内的矩形线圈,其转轴OO′恰好在磁场的边界上.若要线圈中产生感应电流,下列方法中可行的是( )
如图,放在只有右边有边界的匀强磁场内的矩形线圈,其转轴OO′恰好在磁场的边界上.若要线圈中产生感应电流,下列方法中可行的是( )| A. | 线圈绕OO′轴转动 | |
| B. | 线圈绕ab边转动 | |
| C. | 线圈绕ac边转动但不让bd边进入磁场 | |
| D. | 线圈向上平移 |
15.下列各种情况下关于物体所受弹力的受力示意图不正确或不完整的是( )
| A. |  静止在光滑水平面上的小球 | B. |  静止在光滑圆弧面上的杆 | ||
| C. |  静止在光滑斜面上的小球 | D. |  用两段轻绳悬挂着的灯 |
9. 在匀强磁场中,有一接有电容器的回路,如图所示.已知C=30μF,l1=5cm,l2=8cm,磁场以5×10-2T/s的速度增强.则( )
在匀强磁场中,有一接有电容器的回路,如图所示.已知C=30μF,l1=5cm,l2=8cm,磁场以5×10-2T/s的速度增强.则( )
 在匀强磁场中,有一接有电容器的回路,如图所示.已知C=30μF,l1=5cm,l2=8cm,磁场以5×10-2T/s的速度增强.则( )
在匀强磁场中,有一接有电容器的回路,如图所示.已知C=30μF,l1=5cm,l2=8cm,磁场以5×10-2T/s的速度增强.则( )| A. | 电容器上板带正电,带电荷量2×10-9 C | |
| B. | 电容器上板带正电,带电荷量6×10-9 C | |
| C. | 电容器上板带负电,带电荷量4×10-9 C | |
| D. | 电容器上板带负电,带电荷量6×10-9 C |
16.如图所示,两个截面积不同长度相等的均匀铜棒接在电路中,两端电压为U,则( )


| A. | 通过两棒的电流强度相等 | |
| B. | 两棒的自由电子定向移动的平均速率不同 | |
| C. | 两棒内的电场强度不同,细棒内的场强E1大于粗棒内的场强E2 | |
| D. | 细棒两端的电压U1大于粗棒两端的电压U2 |
16. 压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )
压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )
 压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )
压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )| A. | 从t1到t2时间内,小车做匀速直线运动 | |
| B. | 从t1到t2时间内,小车做匀加速直线运动 | |
| C. | 从t2到t3时间内,小车做匀速直线运动 | |
| D. | 从t2到t3时间内,小车做匀加速直线运动 |
 如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s. 如图所示,某导线长L=0.4m(米),通过它的电流I=25A(安培),垂直磁场方向放入B=0.2T(特斯拉)的匀强磁场中,求导线受到安培力的大小和方向?
如图所示,某导线长L=0.4m(米),通过它的电流I=25A(安培),垂直磁场方向放入B=0.2T(特斯拉)的匀强磁场中,求导线受到安培力的大小和方向?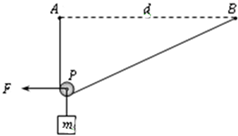 如图所示,将一根长为2d的不可伸长的细绳两端固定在相距为d的AB两等高点,绳上挂一小滑轮P,P下面有一质量为m的物体处于静止状态.现用水平力F拉住滑轮使AP处于竖直方向.若不计绳与滑轮摩擦及空气阻力,也不计绳与滑轮的质量.求水平力F的大小.
如图所示,将一根长为2d的不可伸长的细绳两端固定在相距为d的AB两等高点,绳上挂一小滑轮P,P下面有一质量为m的物体处于静止状态.现用水平力F拉住滑轮使AP处于竖直方向.若不计绳与滑轮摩擦及空气阻力,也不计绳与滑轮的质量.求水平力F的大小.