题目内容
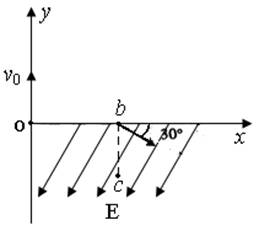
（12分）如图所示，一质量为m，带电量为+q的粒子以速度v0从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从点b处穿过x轴，速度方向与x轴正方向的夹角为300，同时进入场强为E、方向沿与x轴负方向成600角斜向下的匀强电场中，通过了b点正下方的c点，如图所示。粒子的重力不计，试求：
?(1) 圆形匀强磁场区域的最小面积；
?(2) 粒子从O点运动到b的时间；
(3) c点到b点的距离S.
【答案】
（1）带电粒子在磁场中运动时，洛仑兹力提供向心力
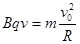……（1分）其运动半径为
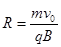……（1分）
带电粒子在磁场中做匀速圆周运动，在磁场区入射点和出射点的弦长为：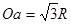
……(2分)
要使圆形匀强磁场区域面积最小，其半径刚好为Oa的一半，则：
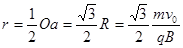…………（1分）其面积为
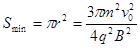………（1分）
（2）带电粒子在磁场中轨迹圆弧对应的圆心角为120°，带电粒子在磁场中运动的时间为圆周运动周期的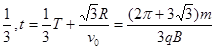
……………………（2分）
（3）带电粒子进入电场后，由于速度方向与静电力方向垂直，故做类平抛运动，
由运动的合成知识有：
S·sin30°=v0t…………（1分） S·cos30°=at2/2…………（1分）
而a=qE/m，联立解得：S=
……………………………（2分）
【解析】略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，一质量为m，带电荷量为+q的小物体，在水平方向的匀强磁场B中，从倾角为
如图所示，一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈，从h1=5m的高处由静止开始下落，然后进入高度为h2（h2＞L）的匀强磁场．下边刚进入磁场时，线圈正好作匀速运动．线圈的下边通过磁场所经历的时间t=0.15s．取g=10m/s2
如图所示，一质量为m的物块恰好沿着倾角为θ的斜面匀速下滑．现对物块施加一个竖直向下的恒力F．则物块（ ）
如图所示，一质量为m的小球，用长为l的轻绳悬挂于O点，小球在水平恒力F的作用下，从最低点A点拉至B点的过程中，力F所做的功为（ ）
如图所示，一质量为m=1.0×10-2kg，带电量为q=1.0×10-6C的小球，用绝缘细线悬挂在水平向右的匀强电场中，假设电场足够大，静止时悬线向左与竖直方向成37°角．小球在运动过程电量保持不变，重力加速度g取10m/s2．