题目内容
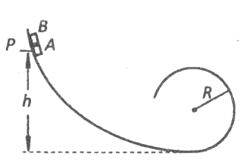
【题目】如图所示,在竖直面内有一个光滑弧形轨道,其末端水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接。A,B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧。两滑块从弧形轨道上的某一高度P点处由静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动恰能通过圆形轨道的最高点,后面的滑块B恰能返回P点。己知圆形轨道的半径![]() ,滑块A的质量
,滑块A的质量![]() ,滑块B的质量
,滑块B的质量![]() ,重力加速度g取
,重力加速度g取![]() ,空气阻力可忽略不计。求:
,空气阻力可忽略不计。求:
(1)滑块A运动到圆形轨道最高点时速度的大小;
(2)两滑块开始下滑时距圆形轨道底端的高度h;
(3)弹簧在将两滑块弹开的过程中释放的弹性势能。
【答案】(1)![]() m/s
m/s
(2)0.8 m
(3)4 J
【解析】
试题(1)设滑块A恰能通过圆形轨道最高点时的速度大小为v2,根据牛顿第二定律有mAg=mA![]()
v2=![]() =
=![]() m/s
m/s
(2)设滑块A在圆形轨道最低点被弹出时的速度大小为v1,对于滑块A从圆形轨道最低点运动到最高点的过程,根据机械能守恒定律,有
![]() mAv12=mAg2R+
mAv12=mAg2R+![]() mAv22
mAv22
v1=6m/s
设滑块A和B运动到圆形轨道最低点速度大小为v0,对滑块A和B下滑到圆形轨道最低点的过程,根据动能定理,有(mA+mB)gh=![]() (mA+mB)v02
(mA+mB)v02
同理滑块B在圆形轨道最低点被弹出时的速度大小也为v0,弹簧将两滑块弹开的过程,对于A、B两滑块所组成的系统水平方向动量守恒,(mA+mB)v0=mA v1-mBv0
解得:h=0.8 m
(3)设弹簧将两滑块弹开的过程中释放的弹性势能为Ep,对于弹开两滑块的过程,根据机械能守恒定律,有![]() (mA+mB)v02 + Ep=
(mA+mB)v02 + Ep=![]() mAv12+
mAv12+![]() mBv02
mBv02
解得:Ep="4" J

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】如图所示,“共享单车”极大地方便了老百姓的出行,某高档“共享单车”通过变速器调整链条在轮盘和飞轮的挂入位置,改变行驶速度。轮盘和飞轮的齿数如下表所示:

名称 | 轮盘 | 飞轮 | |||
A轮 | B轮 | C轮 | D轮 | E轮 | |
齿数N/个 | 48 | 39 | 24 | 18 | 13 |
则下列说法正确的是( )
A.当A轮与C轮组合时,两轮的转速之比为1∶1
B.当A轮与C轮组合时,两轮边缘上的点的线速度大小之比为1∶2
C.当B轮与E轮组合时,两轮角速度之比为1∶3
D.当B轮与E轮组合时,两轮边缘上的点的向心加速度大小之比为3∶1