题目内容
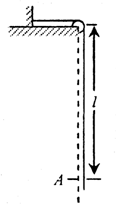如图所示，在一次消防演习中，质量为60kg的消防队员欲到达距离楼顶l=90m处的房间．他沿一条竖直悬垂的轻绳从静止开始匀加速下滑，当他滑到该房间的窗户A处时，突然停止下滑，同时用脚将窗户踢开，自己反弹了一下，然后进入窗内．已知消防员从开始下滑到刚进入窗内共用了时间t=15s，试估算他沿绳子下滑时受到的摩擦力F大小（取1位有效数字）（提示：g取10m/s2，π=3）分析：反弹的过程可以看成单摆的运动，求出单摆运动的周期，从而求出匀加速直线运动的时间．通过匀变速直线运动的位移时间公式求出加速度，通过牛顿第二定律求出摩擦力的大小．
解答：解：单摆的周期T=2π
解得T：=18 s
所以匀加速下滑时间 t′=t-
=6s
根据x=
at2得：
a=
=5m/s2
根据牛顿第二定律得：
mg-F=a
解得：Fmg-ma=3×102N
答：下滑时受到的摩擦力F大小为3×102N
|
解得T：=18 s
所以匀加速下滑时间 t′=t-
| T |
| 2 |
根据x=
| 1 |
| 2 |
a=
| 2l |
| t2 |
根据牛顿第二定律得：
mg-F=a
解得：Fmg-ma=3×102N
答：下滑时受到的摩擦力F大小为3×102N
点评：解决本题的关键不能忽略消防员弹起到进入窗户的时间，结合牛顿第二定律和运动学公式进行求解．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
（2012?许昌模拟）当前，高楼遇险逃生措施及训练引起高度关注．有人设想在消防云梯上再伸出轻便的滑竿解救受困人员，解决云梯高度不够高的问题．如图所示，在一次消防演习中模拟解救被困人员，为了安全，被困人员使用安全带上挂钩挂在滑竿上从高楼A点沿滑杆下滑逃生．滑杆由AO、OB两段直杆通过光滑转轴在O处连接，将被困人员和挂钩理想化为质点，且通过O点的瞬间没有机械能的损失．AO长为L1=5m，OB长为L2=10m．竖直墙与云梯上端点B的间距d=11m．滑杆A端用挂钩钩在高楼的固定物上，可自由转动．B端用铰链固定在云梯上端．挂钩与两段滑杆间动摩擦因数均为μ=0.8．（g=10m/s2）
如图所示，在一次消防演习中，消防员练习使用挂钩从高空沿滑杆由静止滑下，滑杆由AO、OB两段直杆通过光滑转轴连接于O处，现将消防队员和挂钩均理想化为质点，且通过O点的瞬间没有机械能的损失．设AO长为L1=5m，OB长为L2=10m．两堵竖直墙壁的间距d=11m．滑杆A端用铰链固定在墙上．B端用铰链固定在另一侧墙上．挂钩与两段滑杆间动摩擦因数均为μ=0.8．（g=10m/s2，sin37°=0.6，cos37°=0.8）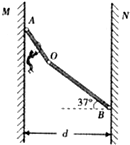
如图所示，在一次消防演习中，消防员练习使用挂钩从高空沿滑杆由静止滑下，滑杆由AO、OB两段直杆通过光滑转轴连接地O处，可将消防员和挂钩均理想化为质点，且通过O点的瞬间没有机械能的损失．AO长为L1=5m，OB长为L2=10m．两堵竖直墙的间距d=11m．滑杆A端用铰链固定在墙上，可自由转动．B端用铰链固定在另一侧墙上．为了安全，消防员到达对面墙的速度大小不能超过6m/s，挂钩与两段滑杆间动摩擦因数均为μ=0.8．（g=10m/s2，sin37°=0.6，cos37°=0.8）．求：
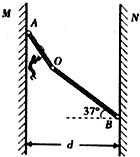如图所示，在一次消防演习中，消防员练习使用挂钩从高空沿滑杆由静止滑下，滑杆由AO、OB两段直杆通过光滑转轴连接地O处，可将消防员和挂钩均理想化为质点，且通过O点的瞬间没有机械能的损失．已知AO长L1=5m，OB长L2=10m，两面竖直墙MN的间距d=11m．滑杆A端用铰链固定在墙上，可自由转动．B端用铰链固定在另一侧墙上．为了安全，消防员到达对面墙的速度大小不能超过6m/s，挂钩与两段滑杆间动摩擦因数均为μ=0.8．（sin37°=0.6，cos37°=0.8）