题目内容
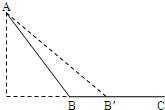（2007?南通模拟）在北戴河旅游景点之一的南戴河滑沙场有两个坡度不同的滑道AB和AB'（均可看作斜面），甲、乙两名旅游者分别乘两个完全相同的滑沙撬从A点由静止开始分别沿AB和AB'滑下，最后都停在水平沙面BC上，如图所示．设滑沙撬和沙面间的动摩擦因数处处相同，斜面与水平面连接处均可认为是圆滑的，滑沙者保持一定姿势坐在滑沙撬上不动．则下列说法中正确的是（ ）分析：根据动能定理求出物体停止时距离A的水平距离，比较出水平距离的大小关系，从而得出运动路程的大小．根据动能定理定理比较B、B′的动能大小．
解答：解：A、设斜面的倾角为θ，根据动能定理得，mgh-μmgcosθs=
mv2-0，因为AB段的水平距离小，则沿AB段到达B点的速率大，由于甲乙两人的质量大小未知，故无法比较动能的大小．故A错误，C正确．
B、对全过程运用动能定理得，mgh-μmgcosθs1-μmgs2=0，整理得，mgh-μmgs水平=0．知沿两轨道滑行水平位移相等．根据几何关系知甲滑行的总路程一定大于乙滑行的总路程．故B正确，D错误．
故选BC．
| 1 |
| 2 |
B、对全过程运用动能定理得，mgh-μmgcosθs1-μmgs2=0，整理得，mgh-μmgs水平=0．知沿两轨道滑行水平位移相等．根据几何关系知甲滑行的总路程一定大于乙滑行的总路程．故B正确，D错误．
故选BC．
点评：本题可以用动力学求解，也可以通过动能定理求解，运用动能定理求解比较简洁．
练习册系列答案
相关题目
（2007?南通模拟）如图甲所示，质量为m=1kg的物体置于倾角为θ=37°的固定斜面上，对物体施以平行于斜面向上的拉力F，t1=1s时撤去拉力，物体运动的部分v-t图象如图乙（sin37°=0.6，cos37°=0.8）试求：
（2007?南通模拟）如图所示，一倾角为30°的光滑斜面底端有一与斜面垂直的固定挡板M，物块A、B之间用一与斜面平行轻质弹簧连结，现用力缓慢沿斜面向下推动物块B，当弹簧具有5J弹性势能时撤去推力释放物块B；已知A、B质量分别为mA=5kg、mB=2kg，弹簧的弹性势能表达式为E
（2007?南通模拟）如图所示，质量m=60kg的高山滑雪运动员，从A点由静止开始沿滑雪道滑下，从B点水平飞出后又落在与水平面成倾角θ=37°的斜坡上C点．已知A、B两点间的高度差为h=25m，B、C两点间的距离为s=75m，已知sin37°=0.6，取g=10m/s2．求：
（2007?南通模拟）如图所示，轻绳两端分别与A、C两物体相连接，mA=1kg，mB=2kg，mC=3kg，物体A、B、C及C与地面间的动摩擦因数均为μ=0.1，轻绳与滑轮间的摩擦可忽略不计，若要用力将C物拉动，则作用在C物上水平向左的拉力最小为（取g=10m/s2）（ ）