题目内容
【题目】一个静止的质量为M的放射性原子核发生衰变，放出一个质量为m、速度大小为v的α粒子，设衰变过程中释放的核能全部转化为新原子核和α粒子的动能，真空中光速为c．求：
①衰变后新原子核速度大小为多少？
②衰变过程中质量亏损为多少？
【答案】①衰变后新原子核速度大小为
；
②衰变过程中质量亏损
【解析】
试题分析：①原子核衰变时动量守恒，由动量守恒定律可以求出衰变后新核的速度大小．
②原子核衰变释放的核能转换为原子核的动能，求出原子核释放的能量，然后由质能方程求出衰变过程中的质量亏损．
解：①衰变过程中动量守恒，选α粒子的速度方向为正，由动量守恒定律得：
mv﹣（M﹣m）v′=0，
解得：
；
②由能量守恒定律得：
，
由E=△mc2，
亏损的质量为：
；
答：①衰变后新原子核速度大小为；
②衰变过程中质量亏损．
练习册系列答案
相关题目
【题目】某同学用伏安法测量导体的电阻，现有量程为3 V、内阻约为3 kΩ的电压表和量程为0．6 A、内阻约为0．1 Ω的电流表。采用分压电路接线，图1是实物的部分连线图，待测电阻为图2中的R1，其阻值约为5 Ω。
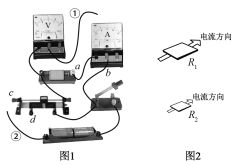
（1）测R1阻值的最优连接方式为导线①连接______（填a或b）、导线②连接______（填c或d）。
（2）正确接线测得实验数据如表，用作图法求得R1的阻值为______Ω。
U/A | 0．40 | 0．80 | 1．20 | 1．60 | 2．00 | 2．40 |
I/A | 0．09 | 0．19 | 0．27 | 0．35 | 0．44 | 0．53 |
（3）已知图2中R2与R1是材料相同、厚度相等、表面为正方形的两导体，R2的边长是R1的
，若测R2的阻值，则最优的连线应选_____（填选项）。
A．①连接a，②连接c B．①连接a，②连接d
C．①连接b，②连接c D．①连接b，②连接d
