题目内容
8.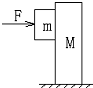 质量为2kg的小木块m与位于光滑水平地面上的质量为4kg的大木块 M接触.两木块之间的动摩擦因数为0.4(最大静摩檫力等于滑动摩擦力),为使小木块与大木块保持相对静止,用一水平力F作用于小木块上,如图所示,则力F的大小至少为( )(g取10m/s2 )
质量为2kg的小木块m与位于光滑水平地面上的质量为4kg的大木块 M接触.两木块之间的动摩擦因数为0.4(最大静摩檫力等于滑动摩擦力),为使小木块与大木块保持相对静止,用一水平力F作用于小木块上,如图所示,则力F的大小至少为( )(g取10m/s2 )| A. | 24N | B. | 50N | C. | 75N | D. | 80N |
分析 为使小木块与大木块保持相对静止,整体必定向右作匀加速运动,且小木块所受的大木块的静摩擦力等于其重力.由摩擦力公式求出M对m的支持力,再对M,由牛顿第二定律求出加速度,最后对整体,由牛顿第二定律求F的最小值.
解答 解:当小木块与大木块恰好保持相对静止时,M对m的静摩擦力恰好达到最大,即有:f=mg
由 f=μN,得:N=$\frac{f}{μ}$=$\frac{mg}{μ}$=$\frac{20}{0.4}$=50N
对M,由牛顿第二定律得:a=$\frac{N}{M}$=$\frac{50}{4}$=12.5m/s2.
对整体则有:F=(M+m)a=(4+2)×12.5N=75N
即力F的大小至少为75N.
故选:C
点评 本题要采用整体法和隔离法选择研究对象,然后平衡条件和牛顿第二定律列式解答.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
12.关于自由落体运动,下列说怯中正确的是( )
| A. | 某段位移内的平均速度等于初速度与末速度和的一半 | |
| B. | 某段时间内的平均速度等于初速度与末速度和的一半 | |
| C. | 在任何相等的时间内速度的变化量相等 | |
| D. | 在任何相等的时间内位移的增量相等 |
3.关于万有引力的下列说法中,正确的是( )
| A. | 两个人擦肩而过,感受不到彼此的吸引力,是因为人与人之间没有万有引力作用 | |
| B. | 运载火箭能从地面加速离开地面,是因为它受到的万有引力近似为零 | |
| C. | 地球绕着太阳运动,是因为地球对太阳的万有引力小于太阳对地球的万有引力 | |
| D. | 月球绕地球运动近似为圆运动,其向心力是地球对月球的万有引力 |
13.自同一点以相同的初速度先后竖直向上抛出两个物体a和b.分别用△h和|△v|表示在同一时刻物体a、b的高度差和速度差的绝对值,在物体b被抛出至两物体相撞这一段时间内( )
| A. | △h不断减小,|△v|也在不断减小 | |
| B. | △h不断减小,|△v|保持不变 | |
| C. | △h在a到达最高点以前保持不变,到达最高点以后不断减小,|△v|始终不断减小 | |
| D. | △h在a到达最高点以前保持不变,到达最高点以后不断减小,|△v|保持不变 |
17.以初速度v=20m/s竖直向上抛一个小球(g=10m/s2),以下说法正确的是( )
| A. | 小球经过4s达到最高点 | |
| B. | 小球上升的最大高度为20m | |
| C. | 小球在出发点上方15m时,速度大小为10m/s | |
| D. | 小球到出发点上方15m时,经过了时间一定是1s |
18.氢原子从n=6跃迁到n=2能级时辐射出频率为v1的光子,从n=5跃迁到n=2能级时辐射出频率为v2的光子.下列说法正确的是( )
| A. | 频率为v1的光子的能量较大 | |
| B. | 频率为v1的光子的动量较大 | |
| C. | 做双缝干涉实验时,频率为v1的光产生的条纹间距较大 | |
| D. | 做光电效应实验时,频率为v1的光产生的光电子的最大初动能较大 |
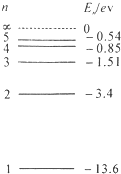 氢原子的能级如图所示,已知可见光的光子能量在1.62ev-3.11ev之间.下列说法正确的是ACD.(填正确答案标号.选对一个得3分,选对2个得4分,选对3个得6分.每选错1个扣3分,最低得分为0分)
氢原子的能级如图所示,已知可见光的光子能量在1.62ev-3.11ev之间.下列说法正确的是ACD.(填正确答案标号.选对一个得3分,选对2个得4分,选对3个得6分.每选错1个扣3分,最低得分为0分)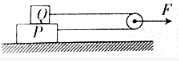 如图所示,重量分别为GP=10N,GQ=110N的物块P、Q叠放在水平地面上,一根绕过动滑轮的轻绳将它们连接在一起.当对动滑轮施加一水平拉力F=60N的作用时,P、Q一起在以相同速度水平向右匀速运动.已知上下两端轻绳处于水平状态,动滑轮的质量及其摩擦均不计,P、Q之间的动摩擦因数μ1=0.4,求:
如图所示,重量分别为GP=10N,GQ=110N的物块P、Q叠放在水平地面上,一根绕过动滑轮的轻绳将它们连接在一起.当对动滑轮施加一水平拉力F=60N的作用时,P、Q一起在以相同速度水平向右匀速运动.已知上下两端轻绳处于水平状态,动滑轮的质量及其摩擦均不计,P、Q之间的动摩擦因数μ1=0.4,求: