题目内容
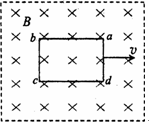
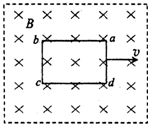
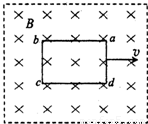
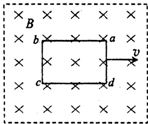将一个闭合矩形金属线框abcd放入如图所示的匀强磁场中，图中虚线表示磁场边界，在用力将线框abcd从磁场中以速度v匀速拉出的过程中，下列说法正确的是（ ）分析：根据q=N
求出通过导线横截面的电量多少．根据能量守恒定律求出拉力做功的大小，判断做功与什么因素有关．
| △Φ |
| R |
解答：解：A、根据q=N
，不管线框的速度如何，磁通量的变化量相同，则通过导线横截面的电量相同．故A错误．
B、根据能量守恒知，拉力做功等于整个回路产生的热量，I=
，则拉力做功W=Q=I2Rt=
R?
=
，知磁场越强，拉力做功越多．拉力做功的多少与线框的宽度bc有关，线框的电阻越多，拉力做功越少．故B正确，C、D错误．
故选B．
| △Φ |
| R |
B、根据能量守恒知，拉力做功等于整个回路产生的热量，I=
| BLbcv |
| R |
| B2Lbc2v2 |
| R2 |
| Lcd |
| v |
| B2Lbc2Lcdv |
| R |
故选B．
点评：本题考查电磁感应与电路和能量的综合，难度中等，需加强这方面的训练．
练习册系列答案
阅读快车系列答案
相关题目
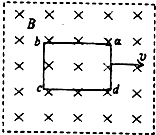将一个闭合矩形金属线框abcd放入如图所示的匀强磁场中，图中虚线表示磁场边界，在用力将线框abcd从磁场以速度v匀速拉出的过程中，下列说法正确的是（ ）| A、拉线框的速度越大，通过导线横截面的电量越多 | B、磁场越强，拉力做的功越多 | C、拉线框的速度越大，拉力的功率越大 | D、线框材料的电阻率越大，拉力做的功越多 |
