题目内容
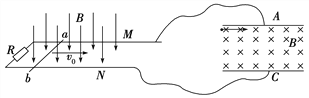
【题目】如图所示，大小为B=1T的水平方向匀强磁场的上下边界分别是MN、PQ，磁场宽度为L=16米，。一个边长为a=1米的正方形导线框从磁场上方竖直下落，线框的质量为m=1Kg，电阻为R=1欧，运动过程中上下两边始终与磁场边界平行，若线框进入磁场过程中感应电流保持不变。（运动过程中空气阻力不计，重力加速度为g=10m/s2）求：
（1）线框下端进入磁场时的速度。
（2）若线框上端离开磁场时线框恰好保持平衡，求线框离开磁场的过程中流经线框电量q和线框完全通过磁场产生的热量Q。
（3）线框下端即将离开磁场时线框的加速度。
【答案】(1) 10m/s （2）
（3）
【解析】试题分析：线框进入磁场过程中感应电流保持不变，说明作匀速运动，由法拉第电磁感应定律、欧姆定律和安培力公式、平衡条件结合，可求得线框下端进入磁场时的速度；当线框上端离开磁场时恰好保持平衡，说明线框受到的安培力与重力相等，则线框上端离开磁场时与线框下端进入磁场时速度相等．根据法拉第电磁感应定律、欧姆定律和电量公式求解电量q．再由能量守恒定律求解热量Q；线框完全进入磁场后做匀加速运动，由运动学速度位移关系公式求解线框下端即将离开磁场时线框的速度，根据牛顿第二定律求解加速度．
（1）由题意可知，线框进入磁场时匀速运动，设线的速度为v1，此过程线圈的重力与安培力平衡，则有： 
，代入数据解得： 
（2）线框离开磁场的过程中流经线框电量q为： 
由题意可知，线框进入磁场时匀速运动，此时重力等于安培力，线框上端离开磁场时线框恰好保持平衡，也有重力等于安培力。由此可知动能变化量为零。根据能量守恒可得： 
（3）线框完全进入磁场后做匀加速运动，设线框下端即将离开磁场时速度为v2，则
此时线框受到的安培力为： 
、重力mg，则加速度为
，联立解得： 
练习册系列答案
黄冈冠军课课练系列答案
相关题目
