题目内容
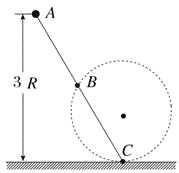
【题目】如图所示为某款弹射游戏示意图,光滑水平台面上固定发射器、竖直光滑圆轨道和粗糙斜面![]() ,竖直面
,竖直面![]() 和竖直靶板
和竖直靶板![]() 。通过轻质拉杆将发射器的弹簧压缩一定距离后释放,滑块从
。通过轻质拉杆将发射器的弹簧压缩一定距离后释放,滑块从![]() 点弹出并从
点弹出并从![]() 点进人圆轨道,绕转一周后继续在平直轨道上前进,从
点进人圆轨道,绕转一周后继续在平直轨道上前进,从![]() 点沿斜面
点沿斜面![]() 向上运动,滑块从
向上运动,滑块从![]() 点射向靶板目标(滑块从水平面滑上斜面时不计能量损失)。已知滑块质量
点射向靶板目标(滑块从水平面滑上斜面时不计能量损失)。已知滑块质量![]() ,斜面倾角
,斜面倾角![]() ,斜面长
,斜面长![]() ,滑块与斜面
,滑块与斜面![]() 之间的动摩擦因数
之间的动摩擦因数![]() ,竖直面
,竖直面![]() 与靶板
与靶板![]() 间距离为
间距离为![]() ,
,![]() 点离靶板上
点离靶板上![]() 环中心点
环中心点![]() 的竖直距离
的竖直距离![]() ,忽略空气阻力,滑块可视为质点。已知
,忽略空气阻力,滑块可视为质点。已知![]() ,取
,取![]() ,求:
,求:

(1)若要使滑块恰好能够到达![]() 点,则圆轨道允许的最大半径为多大?
点,则圆轨道允许的最大半径为多大?
(2)在另一次弹射中发现滑块恰能水平击中靶板上的![]() 点,则此次滑块被弹射前弹簧被压缩到最短时的弹性势能为多大? (结果保留三位有效数字)
点,则此次滑块被弹射前弹簧被压缩到最短时的弹性势能为多大? (结果保留三位有效数字)
(3)若![]() 板可沿水平方向左右移动靠近或远高斜面,以保证滑块从
板可沿水平方向左右移动靠近或远高斜面,以保证滑块从![]() 点出射后均能水平击中靶板。以
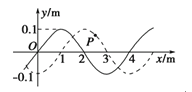
点出射后均能水平击中靶板。以![]() 点为坐标原点,建立水平竖直坐标系(如图) ,则滑块水平击中靶板位置坐标
点为坐标原点,建立水平竖直坐标系(如图) ,则滑块水平击中靶板位置坐标![]() 应满足什么条件?
应满足什么条件?
【答案】(1)![]() (2)
(2) ![]() (3)
(3)![]() ,或
,或![]() ,或
,或![]()
【解析】(1)设圆轨道允许的半径最大值为![]()
在圆轨道最高点:![]()
要使滑块恰好能到达![]() 点,即:
点,即:![]()
从圆轨道最高点至![]() 点的过程:
点的过程:![]()
代入数据可得![]()
(2)滑块恰能水平击中靶板上的![]() 点,
点,![]() 到
到![]() 运动的逆过程为平抛运动
运动的逆过程为平抛运动
从![]() 到
到![]() :
:![]()
代入数据可得:![]()
从弹射至点的过程:![]()
代入数据可得:![]()
(3)同理根据平抛规律可知:![]()
即![]() ,或
,或![]() ,或
,或![]()

练习册系列答案
相关题目