题目内容
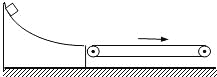
【题目】如图所示,放置在竖直平面内的光滑杆AB,是按照从高度为h处以初速度![]() 平抛的运动轨迹制成的,A端为抛出点,B端为落地点。现将一小球套于其上,由静止开始从轨道A端滑下。已知重力加速度为g,当小球到达轨道B端时
平抛的运动轨迹制成的,A端为抛出点,B端为落地点。现将一小球套于其上,由静止开始从轨道A端滑下。已知重力加速度为g,当小球到达轨道B端时![]()
![]()

A. 小球的速率为![]()
B. 小球的速率为![]()
C. 小球在水平方向的速度大小为![]()
D. 小球在水平方向的速度大小为![]()
【答案】BD
【解析】
试题由于杆AB光滑,小球在整个运动过程中,受重力mg和杆的弹力N作用,又由于弹力N始终与小球运动的速度相垂直,因此一直不做功,根据动能定理有:mgh=![]() -0,解得小球到达轨道B端时的速率为v=
-0,解得小球到达轨道B端时的速率为v=![]() ,故选项A错误;选项B正确;由于杆AB是按照从高度为h处以初速度v0平抛的运动轨迹制成的,不妨假设B端的切线方向与水平方向间的夹角为θ,当物体以初速度v0平抛运动至B端时,根据动能定理有:mgh=
,故选项A错误;选项B正确;由于杆AB是按照从高度为h处以初速度v0平抛的运动轨迹制成的,不妨假设B端的切线方向与水平方向间的夹角为θ,当物体以初速度v0平抛运动至B端时,根据动能定理有:mgh=![]() -
-![]() ,解得:v′=
,解得:v′=![]() ,根据几何关系有:cosθ=
,根据几何关系有:cosθ=![]() =
=![]() ,所以小球沿杆到达轨道B端在水平方向的速度大小为:vx=vcosθ=
,所以小球沿杆到达轨道B端在水平方向的速度大小为:vx=vcosθ=![]() ,故选项C错误;选项D正确。
,故选项C错误;选项D正确。

练习册系列答案
相关题目