题目内容
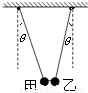
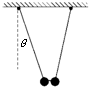 如图所示,甲、乙是摆长相同的两个单摆,它们中间用一根细线相连,两摆线均与竖直方向成θ角.已知甲的质量大于乙的质量,当细线突然断开后,两物块都做简谐运动,在摆动过程中( )
如图所示,甲、乙是摆长相同的两个单摆,它们中间用一根细线相连,两摆线均与竖直方向成θ角.已知甲的质量大于乙的质量,当细线突然断开后,两物块都做简谐运动,在摆动过程中( )分析:根据能量守恒定律判断出它们上升的最大高度相同.单摆的周期T=2π
,周期与摆球的质量、振幅无关.
|
解答:解:根据能量守恒定律判断出它们上升的最大高度相同、振幅相同.根据单摆的周期T=2π
,周期与摆球的质量、振幅无关.
根据动能定理,由最高点到最低点,mgl(1-cosθ)=
mv2-0=
,所以甲乙最大速度相等.故D正确,A、B、C错误.
故选D.
|
根据动能定理,由最高点到最低点,mgl(1-cosθ)=
| 1 |
| 2 |
| 2gl(1-cosθ) |
故选D.
点评:解决本题的关键掌握单摆的周期公式T=2π
,以及会熟练运用能量守恒、动能定理、机械能守恒定律.
|

练习册系列答案
相关题目
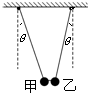 (2010?奉贤区一模)如图所示,甲、乙是摆长相同的两个单摆,它们中间用一根细线相连,两摆线均与竖直方向成θ角.已知甲的质量小于乙的质量,当细线突然断开后,甲、乙两摆都做简谐运动,下列说法正确的是( )
(2010?奉贤区一模)如图所示,甲、乙是摆长相同的两个单摆,它们中间用一根细线相连,两摆线均与竖直方向成θ角.已知甲的质量小于乙的质量,当细线突然断开后,甲、乙两摆都做简谐运动,下列说法正确的是( )