题目内容
 (适合于“侧重理论”的考生).如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为6kg?m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4kg?m/s,则左方是
(适合于“侧重理论”的考生).如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为6kg?m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4kg?m/s,则左方是A
A
球,碰撞后A、B两球速度大小之比为2:5
2:5
.分析:两球碰撞过程,系统不受外力,故碰撞过程系统总动量守恒;
同时考虑实际情况,碰撞前后面的球速度大于前面球的速度.
动量是矢量,具有方向性.
同时考虑实际情况,碰撞前后面的球速度大于前面球的速度.
动量是矢量,具有方向性.
解答:解:规定向右为正方向,碰撞前A、B两球的动量均为6kg?m/s,说明A、B两球的速度方向向右,
两球质量关系为mB=2mA,所以碰撞前vA>vB,所以左方是A球.
碰撞后A球的动量增量为-4kg?m/s,所以碰撞后A球的动量是2kg?m/s
碰撞过程系统总动量守恒,mAvA+mBvB=-mAvA′+mBvB′
所以碰撞后B球的动量是10kg?m/s
根据mB=2mA,所以碰撞后A、B两球速度大小之比为2:5.
故答案为:A,2:5.
两球质量关系为mB=2mA,所以碰撞前vA>vB,所以左方是A球.
碰撞后A球的动量增量为-4kg?m/s,所以碰撞后A球的动量是2kg?m/s
碰撞过程系统总动量守恒,mAvA+mBvB=-mAvA′+mBvB′
所以碰撞后B球的动量是10kg?m/s
根据mB=2mA,所以碰撞后A、B两球速度大小之比为2:5.
故答案为:A,2:5.
点评:碰撞过程中动量守恒,同时要遵循能量守恒定律,不忘联系实际情况,即后面的球不会比前面的球运动的快!
由于动量是矢量,具有方向性,在讨论动量守恒时必须注意到其方向性.为此首先规定一个正方向,然后在此基础上进行研究.
由于动量是矢量,具有方向性,在讨论动量守恒时必须注意到其方向性.为此首先规定一个正方向,然后在此基础上进行研究.

练习册系列答案
相关题目
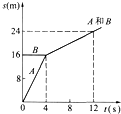 (适合于“侧重理论”的考生)A、B两物体在光滑的水平面上发生碰撞,碰撞前后物体的运动都在同一条直线上.规定A物体原运动方向为正方向.A物体的质量mA=0.5kg.若不计碰撞时间,它们碰撞前后的位移图象如图所示.碰撞前B的质量为mB=
(适合于“侧重理论”的考生)A、B两物体在光滑的水平面上发生碰撞,碰撞前后物体的运动都在同一条直线上.规定A物体原运动方向为正方向.A物体的质量mA=0.5kg.若不计碰撞时间,它们碰撞前后的位移图象如图所示.碰撞前B的质量为mB=

