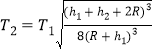题目内容
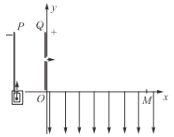
【题目】如图所示,在光滑水平面上有一质量为2018m的木板,板上有2018块质量均为m的相同木块1、2、…、2018。最初木板静止,各木块分别以v、2v、…、2018v同时向同一方向运动,木块和木板间的动摩擦因数为μ,且木块间不发生碰撞和离开木板的现象。求:

(1)最终木板的速度
(2)第一块木块相对木板滑动的时间
(3)运动中第88块木块的最小速度。
【答案】(1) ![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)设当所有物块的速度相等时的速度为v′,选取向右为正方向,则有:
m(v+2v+3v+…+nv)=2nmv′
可得:v′=![]()
(2)第一块木块:木块:![]() ;
; ![]()
木板:![]() ;
;![]()
共速时:v1=v1′
解得![]()
共同速度v2=![]() v
v
(3)设第k块木块的最小速度为vk,则此时木块与第1至第k-1块木块的速度均为vk,由于所有的木块的质量都相等,所以所有的木块受到的摩擦力大小都是相等的,设为μmg,由动量定理可知,在相等的时间内,第k+1块木块至第n块木块速度的减小量也相等,因而此时第k+1块木块至第n块木块速度依次是:
vk+v,vk+2v,vk+3v…vk+(n-k)v
则由动量守恒定律可得:

练习册系列答案
相关题目