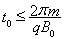Question

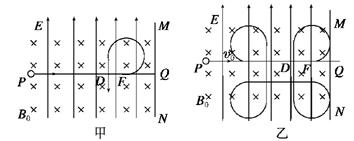
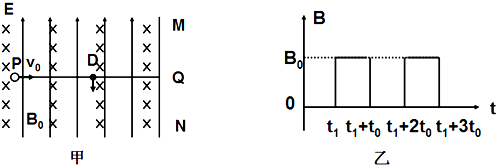
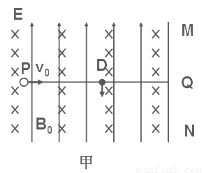
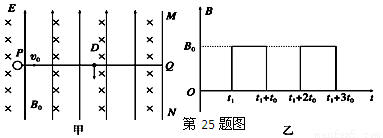
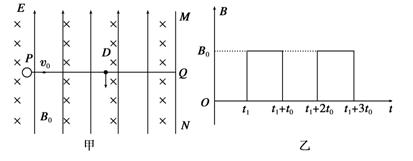
如图甲所示，竖直面MN的左侧空间存在竖直向上的匀强电场(上、下及左侧无边界)．一个质量为m、电荷量为q的可视为质点的带正电的小球，以大小为v₀的速度垂直于竖直面MN向右做直线运动．小球在t＝0时刻通过电场中的P点，为使小球能在以后的运动中竖直向下通过D点(P、D间距为L，且它们的连线垂直于竖直平面MN，D到竖直面MN的距离DQ等于L/π)，经过研究，可以在电场所在的空间叠加如图乙所示的随时间周期性变化的、垂直于纸面向里的磁场．(g＝10m/s²)，求：

(1)场强E的大小；

(2)如果磁感应强度B₀为已知量，试推出满足条件t₁的表达式；

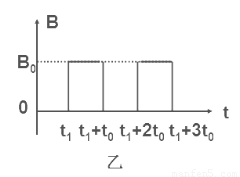
(3)进一步的研究表明，竖直向下的通过D点的小球将做周期性运动．则当小球运动的周期最大时，求出磁感应强度B₀及运动的最大周期T的大小，并在图中定性地画出小球运动一个周期的轨迹．(只需要画出一种可能的情况)

Answer 1

(1)mg/q　(2)＋　(3)　　轨迹见解析图乙

解析:

(1)小球进入电场，做匀速直线运动时

Eq＝mg，①

E＝mg/q.②

(2)在t₁时刻加磁场，小球在时间t₀内做匀速圆周运动(如图甲所示)，设圆周运动的周期为T₀，半径为R₀.

竖直向下通过D点，则t₀＝3T₀/4，      ③

B₀qv₀＝m④

PF－PD＝R即v₀t₁－L＝R，            ⑤

将③④代入⑤式解得t₁＝＋.

(3)小球运动的速率始终不变，当R变大时，T₀也增加，小球在电场中的运动周期T也增加

在小球不飞出电场的情况下，当T₀最大时，有：

DQ＝2R，即＝，               ⑥

T₀＝＝，                     ⑦

结合⑥⑦式是B₀＝，

T₀＝.

结合轨迹图可知，小球在电场中运动的最大周期T＝4×(＋t₀)．

结合上式解得T＝.

所以小球在电场中运动一个周期的轨迹如图乙所示．