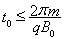题目内容
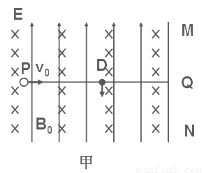
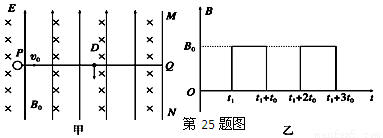
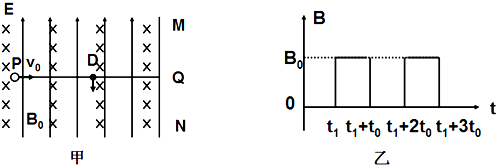
如图甲所示,竖直面MN的左侧空间存在竖直向上的匀强电场(上、下及左侧无边界).一个质量为m、电量为q的可视为质点的带正电的小球,以大小为V
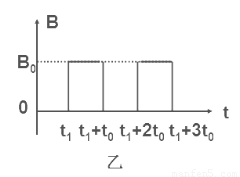
0的速度垂直于竖直面MN向右作直线运动.小球在t=0时刻通过电场中的P点,为使小球能在以后的运动中竖直向下通过D点(P、D间距为L,且它们的连线垂直于竖直平面MN,D到竖直面MN的距离DQ等于L/π),经过研究,可以在电场所在的空间叠加如图乙所示随时间周期性变化的、垂直纸面向里的磁场.(g=10m/s
2)求:
(1)场强E的大小;
(2)如果磁感应强度B
0为已知量,试推出满足条件t
1的表达式;
(3)进一步的研究表明,竖直向下的通过D点的小球将做周期性运动.则当小球运动的周期最大时,求出磁感应强度B
0及运动的最大周期T的大小,并在图中定性画出小球运动一个周期的轨迹(只需要画出一种可能的情况)
分析:(1)小球受到电场力与重力相平衡,即可求解;
(2)根据洛伦兹力提供向心力,结合几何关系,从而即可求解;
(3)小球运动的速率始终不变,当R变大时,T0也增加,由周期公式结合长度关系,可求出磁感应强度,由运动轨迹,可求出最大周期.并画出运动轨迹.
解答:解:(1)小球进入电场,做匀速直线运动时 Eq=mg①
解得:E=
②
(2)在t
1时刻加磁场,小球在时间t
0内做匀速圆周运动,设圆周运动周期为T
0,半径为R.
竖直向下通过D点,则:t
0=
T
0 ③
Bqv0=m④
PF-PD=R
即v
0t
1-L=R⑤
将③、④代入⑤式解得:
t1=+⑥
(3)小球运动的速率始终不变,当R变大时,T
0也增加,小球在电场中的运动周期T也增加.
在小球不飞出电场的情况下,当T最大时,有:
DQ=2R 即
=⑥
T0==⑦
结合⑥⑦式解得:
B0=⑧
T0=⑨
结合轨迹图可知,小球在电场中运动的最大周期,
T=4×(+t0)⑩
结合上式解得:
T=小球在电场中运动一个周期的轨迹图如图所示;

答:(1)场强E的大小E=
;
(2)如果磁感应强度B
0为已知量,试推出满足条件t
1的表达式得:
t1=+;
(3)磁感应强度B
0及运动的最大周期T的大小:
T=,小球运动一个周期的轨迹如上图所示.
点评:考查粒子受到电场力与洛伦兹力作用,涉及匀速直线运动与匀速圆周运动,掌握平衡方程与牛顿第二定律的方程,注意几何知识在题中的应用,并掌握运动轨迹的对称性.
练习册系列答案
相关题目