��Ŀ����
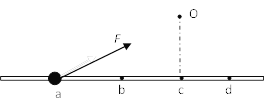
����Ŀ���뾶ΪR�����ȴ�����ɵ������ڿռ������ԳƵĵ糡����ǿ��С�ذ뾶�ֲ���ͼ��ʾ��ͼ��E0��֪��E��r������O��R���ֵ��������R��2R���ֵ������

��1��д��E��r����������ĵ�λ��
��2����֪��������r��R���ij�ǿE=![]() ��ʽ��kΪ�������������þ��ȴ����������ĵ����QΪ���
��ʽ��kΪ�������������þ��ȴ����������ĵ����QΪ���
��3����������������ĵ��Ʋ���U��
��4������Ϊm�������Ϊq�ĸ���������洦����ж����ٶȿ��Ըպ��˶���2R����
���𰸡���1��E��r����������ĵ�λΪV
��2���þ��ȴ����������ĵ����QΪ![]() ��
��
��3��������������ĵ��Ʋ�Ϊ![]() ��
��
��4������Ϊm�������Ϊq�ĸ���������洦�����![]() ���ٶȿ��Ըպ��˶���2R����
���ٶȿ��Ըպ��˶���2R����
���������⣺��1��E��r�����������ʾ���Ʋ��λΪV��
��2������R���ij�ǿΪE0����![]() �����Q=
�����Q=![]() ��
��
��3��E��r������Χ�ɵ������ʾ���Ʋ��������������ĵ��Ʋ���U=![]() ��
��
��4��E��r������O��R���ֵ��������R��2R���ֵ������֪������2R���ĵ��Ʋ��СΪ![]()
���ݶ��ܶ����ã�![]()
���![]() ��
��
�𣺣�1��E��r����������ĵ�λΪV
��2���þ��ȴ����������ĵ����QΪ![]() ��
��
��3��������������ĵ��Ʋ�Ϊ![]() ��
��
��4������Ϊm�������Ϊq�ĸ���������洦�����![]() ���ٶȿ��Ըպ��˶���2R����
���ٶȿ��Ըպ��˶���2R����