题目内容
如右图所示,用轻弹簧相连的质量均为2 kg的A、B两物块都以v="6" m/s的速度在光滑水平地面上运动,弹簧处于原长,质量4 kg的物块C静止在前方,B与C碰撞后二者粘在一起运动。在以后的运动中,求:

(1)当弹簧的弹性势能最大时,物体A的速度多大?
(2)弹性势能的最大值是多大?

(1)当弹簧的弹性势能最大时,物体A的速度多大?
(2)弹性势能的最大值是多大?
(1)3m/s(2)12J
试题分析:(1)当A、B、C三者的速度相等时弹簧的弹性势能最大.
由于A、B、C三者组成的系统动量守恒:
(mA+mB)v=(mA+mB+mC)vA′ ①
由①式解得 vA′="3" (m/s) ②
(2) B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为v′,则:
mBv=(mB+mC)v′③
由③式解得: v′=2(m/s) ④
设物A速度为vA′时,弹簧的弹性势能最大为Ep,根据能量守恒:
Ep=
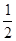 (mB+mC)
(mB+mC)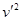 +
+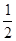 mAv2-
mAv2-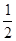 (mA+mB+mC)
(mA+mB+mC) 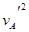 ⑤
⑤ 由⑤ 式解得:Ep=12(J)⑥
点评:本题考查了碰撞过程中的动量守恒定律以及系统的能量守恒定律问题。在运用过程中要注意动量守恒定律的前提条件。

练习册系列答案
相关题目
 )和一个氚核(
)和一个氚核( )结合成一个氦核并放出一个中子时,质量亏损为
)结合成一个氦核并放出一个中子时,质量亏损为 m,已知阿伏加德罗常数为NA,真空中的光速为c,若1mol氘和1mol氚完全发生上述核反应,则在核反应中释放的能量为________。
m,已知阿伏加德罗常数为NA,真空中的光速为c,若1mol氘和1mol氚完全发生上述核反应,则在核反应中释放的能量为________。 核轰击质量为m2的静止的
核轰击质量为m2的静止的 核,发生核反应,最终产生两种新粒子A和B。其中A为
核,发生核反应,最终产生两种新粒子A和B。其中A为 核,质量为m3,速度为v3;B的质量为m4。粒子A的速度符合条件_________时,粒子B的速度方向与He核的运动方向相反。
核,质量为m3,速度为v3;B的质量为m4。粒子A的速度符合条件_________时,粒子B的速度方向与He核的运动方向相反。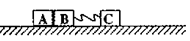

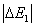 和
和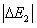 ,下列关于原子这两次跃迁的说法中正确的是( )
,下列关于原子这两次跃迁的说法中正确的是( )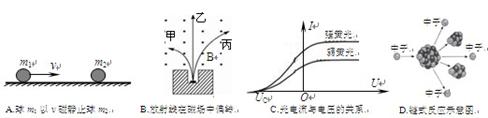
 粒子流,具有很强的穿透能力
粒子流,具有很强的穿透能力